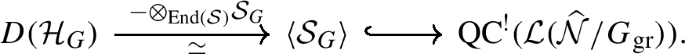
Coherent Springer theory and the categorical Deligne-Langlands correspondence

Abstract Kazhdan and Lusztig identified the affine Hecke algebra ℋ with an equivariant $K$ K -group of the Steinberg variety, and applied this to prove the Deligne-Langlands conjecture, i.e., the local Langlands parametrization of irreducible representations of reductive groups over nonarchimedean local fields $F$ F with an Iwahori-fixed vector. We apply techniques from derived algebraic geometry to pass from $K$ K -theory to Hochschild homology and thereby identify ℋ with the endomorphisms of a coherent sheaf on the stack of unipotent Langlands parameters, the coherent Springer sheaf . As a result the derived category of ℋ-modules is realized as a full subcategory of coherent sheaves on this stack, confirming expectations from strong forms of the local Langlands correspondence (including recent conjectures of Fargues-Scholze, Hellmann and Zhu). In the case of the general linear group our result allows us to lift the local Langlands classification of irreducible representations to a categorical statement: we construct a full embedding of the derived category of smooth representations of $\mathrm{GL}_{n}(F)$ GL n ( F ) into coherent sheaves on the stack of Langlands parameters.