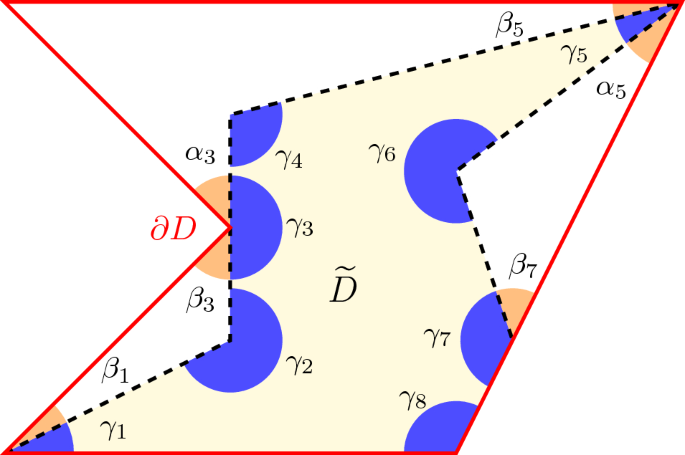
Heat Flow in Polygons with Reflecting Edges

Abstract We investigate the heat flow in an open, bounded set D in $$\mathbb {R}^2$$ R 2 with polygonal boundary $$\partial D$$ ∂ D . We suppose that D contains an open, bounded set $$\widetilde{D}$$ D ~ with polygonal boundary $$\partial \widetilde{D}$$ ∂ D ~ . The initial condition is the indicator function of $$\widetilde{D}$$ D ~ and we impose a Neumann boundary condition on the edges of $$\partial D$$ ∂ D . We obtain an asymptotic formula for the heat content of $$\widetilde{D}$$ D ~ in D as time $$t\downarrow 0$$ t ↓ 0 .