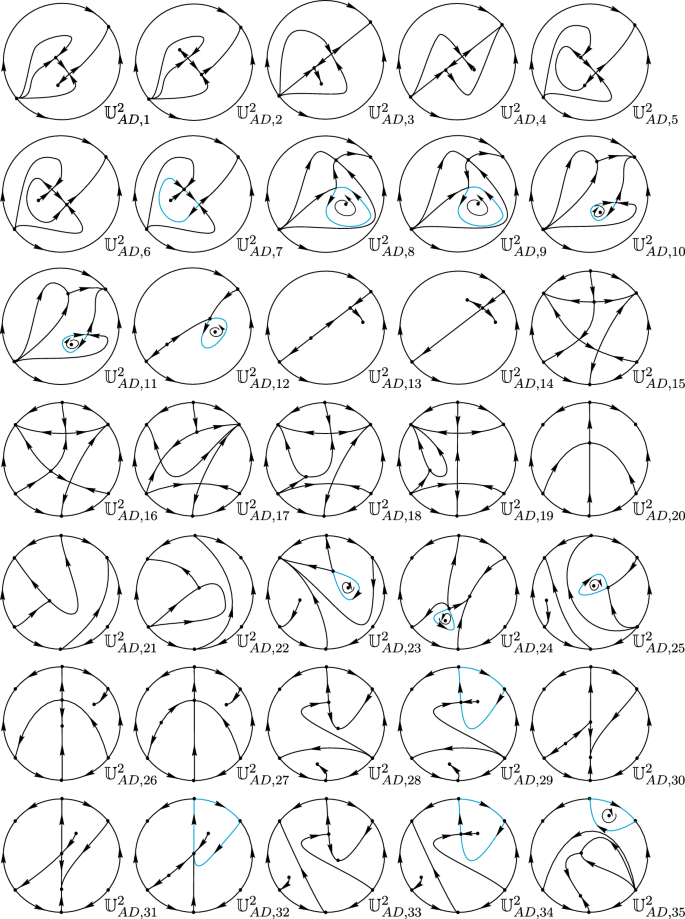
Structurally Unstable Quadratic Vector Fields of Codimension Two: Families Possessing One Finite Saddle-Node and a Separatrix Connection

Abstract This paper is part of a series of works whose ultimate goal is the complete classification of phase portraits of quadratic differential systems in the plane modulo limit cycles. It is estimated that the total number may be around 2000, so the work to find them all must be split in different papers in a systematic way so to assure the completeness of the study and also the non intersection among them. In this paper we classify the family of phase portraits possessing one finite saddle-node and a separatrix connection and determine that there are a minimum of 77 topologically different phase portraits plus at most 16 other phase portraits which we conjecture to be impossible. Along this paper we also deploy a mistake in the book (Artés et al. in Structurally unstable quadratic vector fields of codimension one, Birkhäuser/Springer, Cham, 2018) linked to a mistake in Reyn and Huang (Separatrix configuration of quadratic systems with finite multiplicity three and a $$M^0_{1,1}$$ M 1 , 1 0 type of critical point at infinity. Report Technische Universiteit Delft, pp 95–115, 1995).