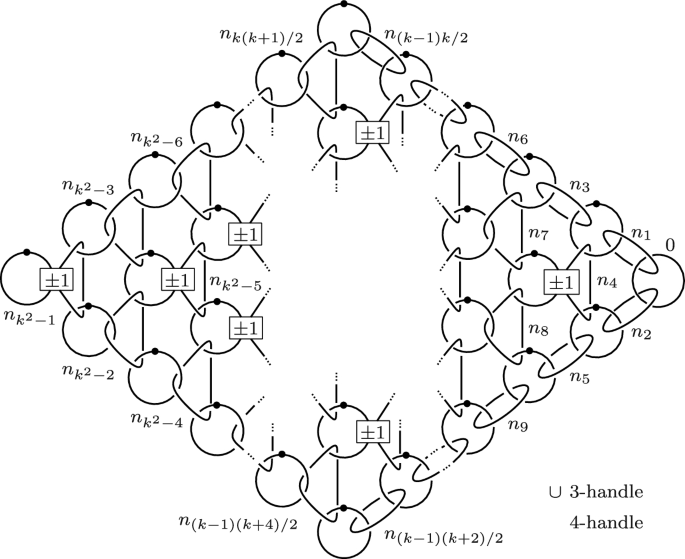
Constructions of homotopy 4-spheres by pochette surgery

Abstract The boundary sum of the product of a circle with a 3-ball and the product of a disk with a 2-sphere is called a pochette. Pochette surgery, which was discovered by Iwase and Matsumoto, is a generalization of Gluck surgery and a special case of torus surgery. For a pochette P embedded in a 4-manifold X , a pochette surgery on X is the operation of removing the interior of P and gluing P by a diffeomorphism of the boundary of P . We present an explicit diffeomorphism of the boundary of P for constructing a 4-manifold after any pochette surgery. We also describe a necessary and sufficient condition for some pochette surgeries on any simply-connected closed 4-manifold create a 4-manifold with the same homotopy type of the original 4-manifold. In this paper we construct infinitely many embeddings of a pochette into the 4-sphere and prove that homotopy 4-spheres obtained from surgeries along these embedded pochettes are all diffeomorphic to the 4-sphere by some explicit handle calculus and relative handle calculus.