二维正向和反向跃迁速率

IF 0.8 Q4 BUSINESS, FINANCE

European Actuarial Journal Pub Date : 2023-10-07 DOI:10.1007/s13385-023-00363-3

Theis Bathke, Marcus C. Christiansen

{"title":"二维正向和反向跃迁速率","authors":"Theis Bathke, Marcus C. Christiansen","doi":"10.1007/s13385-023-00363-3","DOIUrl":null,"url":null,"abstract":"Abstract Forward transition rates were originally introduced with the aim to evaluate life insurance liabilities market-consistently. While this idea turned out to have its limitations, recent literature repurposes forward transition rates as a tool for avoiding Markov assumptions in the calculation of life insurance reserves. While life insurance reserves are some form of conditional first-order moments, the calculation of conditional second-order moments needs an extension of the forward transition rate concept from one dimension to two dimensions. Two-dimensional forward transition rates are also needed for the calculation of path-dependent life insurance cash-flows as they occur upon contract modifications. Forward transition rates are designed for doing prospective calculations, and by a time-symmetric definition of so-called backward transition rates one can do retrospective calculations.","PeriodicalId":44305,"journal":{"name":"European Actuarial Journal","volume":null,"pages":null},"PeriodicalIF":0.8000,"publicationDate":"2023-10-07","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Two-dimensional forward and backward transition rates\",\"authors\":\"Theis Bathke, Marcus C. Christiansen\",\"doi\":\"10.1007/s13385-023-00363-3\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"Abstract Forward transition rates were originally introduced with the aim to evaluate life insurance liabilities market-consistently. While this idea turned out to have its limitations, recent literature repurposes forward transition rates as a tool for avoiding Markov assumptions in the calculation of life insurance reserves. While life insurance reserves are some form of conditional first-order moments, the calculation of conditional second-order moments needs an extension of the forward transition rate concept from one dimension to two dimensions. Two-dimensional forward transition rates are also needed for the calculation of path-dependent life insurance cash-flows as they occur upon contract modifications. Forward transition rates are designed for doing prospective calculations, and by a time-symmetric definition of so-called backward transition rates one can do retrospective calculations.\",\"PeriodicalId\":44305,\"journal\":{\"name\":\"European Actuarial Journal\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.8000,\"publicationDate\":\"2023-10-07\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"European Actuarial Journal\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://doi.org/10.1007/s13385-023-00363-3\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"BUSINESS, FINANCE\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"European Actuarial Journal","FirstCategoryId":"1085","ListUrlMain":"https://doi.org/10.1007/s13385-023-00363-3","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"BUSINESS, FINANCE","Score":null,"Total":0}

引用次数: 0

摘要

摘要引入远期过渡利率的初衷是为了评估寿险负债的市场一致性。虽然这一想法被证明有其局限性，但最近的文献重新将远期过渡率作为一种工具，以避免在计算人寿保险准备金时使用马尔可夫假设。寿险准备金是某种形式的条件一阶矩，而条件二阶矩的计算需要将前向转移率的概念从一维扩展到二维。二维远期转移率也需要用于计算路径依赖的人寿保险现金流，因为它们发生在合同修改后。前向转换速率是为进行前瞻性计算而设计的，而根据所谓的后向转换速率的时间对称定义，人们可以进行回顾性计算。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

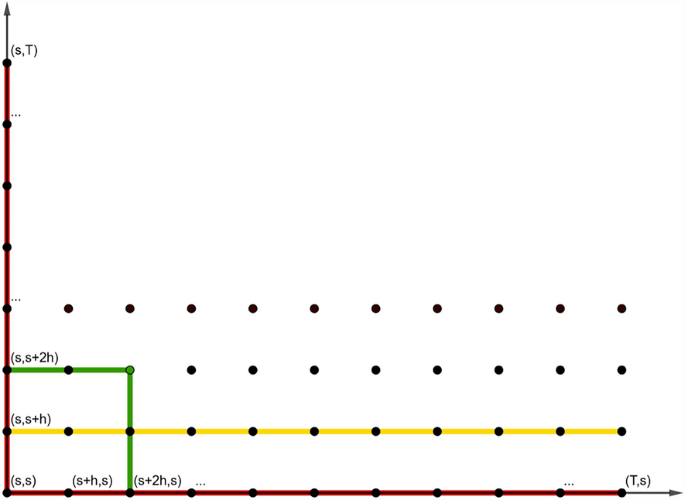
Two-dimensional forward and backward transition rates

查看原文本刊更多论文

Two-dimensional forward and backward transition rates

Abstract Forward transition rates were originally introduced with the aim to evaluate life insurance liabilities market-consistently. While this idea turned out to have its limitations, recent literature repurposes forward transition rates as a tool for avoiding Markov assumptions in the calculation of life insurance reserves. While life insurance reserves are some form of conditional first-order moments, the calculation of conditional second-order moments needs an extension of the forward transition rate concept from one dimension to two dimensions. Two-dimensional forward transition rates are also needed for the calculation of path-dependent life insurance cash-flows as they occur upon contract modifications. Forward transition rates are designed for doing prospective calculations, and by a time-symmetric definition of so-called backward transition rates one can do retrospective calculations.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

European Actuarial Journal BUSINESS, FINANCE-

CiteScore

2.30

自引率

8.30%

发文量

期刊介绍： Actuarial science and actuarial finance deal with the study, modeling and managing of insurance and related financial risks for which stochastic models and statistical methods are available. Topics include classical actuarial mathematics such as life and non-life insurance, pension funds, reinsurance, and also more recent areas of interest such as risk management, asset-and-liability management, solvency, catastrophe modeling, systematic changes in risk parameters, longevity, etc. EAJ is designed for the promotion and development of actuarial science and actuarial finance. For this, we publish original actuarial research papers, either theoretical or applied, with innovative applications, as well as case studies on the evaluation and implementation of new mathematical methods in insurance and actuarial finance. We also welcome survey papers on topics of recent interest in the field. EAJ is the successor of six national actuarial journals, and particularly focuses on links between actuarial theory and practice. In order to serve as a platform for this exchange, we also welcome discussions (typically from practitioners, with a length of 1-3 pages) on published papers that highlight the application aspects of the discussed paper. Such discussions can also suggest modifications of the studied problem which are of particular interest to actuarial practice. Thus, they can serve as motivation for further studies.Finally, EAJ now also publishes ‘Letters’, which are short papers (up to 5 pages) that have academic and/or practical relevance and consist of e.g. an interesting idea, insight, clarification or observation of a cross-connection that deserves publication, but is shorter than a usual research article. A detailed description or proposition of a new relevant research question, short but curious mathematical results that deserve the attention of the actuarial community as well as novel applications of mathematical and actuarial concepts are equally welcome. Letter submissions will be reviewed within 6 weeks, so that they provide an opportunity to get good and pertinent ideas published quickly, while the same refereeing standards as for other submissions apply. Both academics and practitioners are encouraged to contribute to this new format. Authors are invited to submit their papers online via http://euaj.edmgr.com.