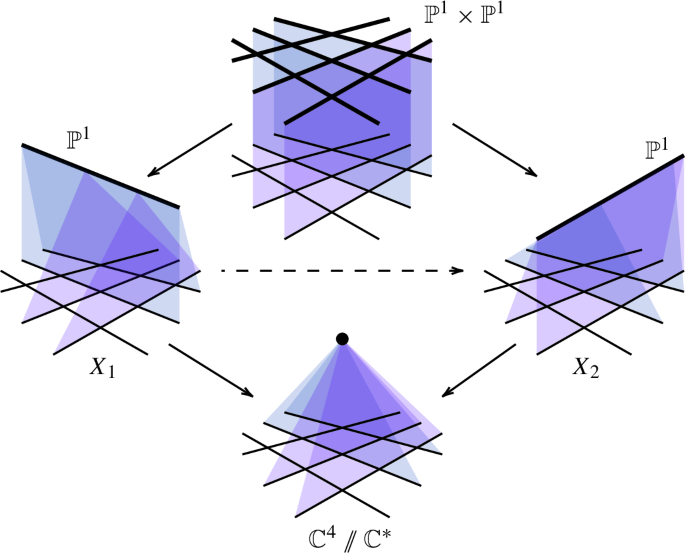
Morelli-Włodarczyk cobordism and examples of rooftop flips

Abstract We introduce the notion of rooftop flip, namely a small modification among normal projective varieties which is modeled by a smooth projective variety of Picard number 2 admitting two projective bundle structures. Examples include the Atiyah flop and the Mukai flop, modeled respectively by $$\mathbb {P}^1\times \mathbb {P}^1$$ P 1 × P 1 and by $$\mathbb {P}\left( T_{\mathbb {P}^2}\right) $$ P T P 2 . Using the Morelli-Włodarczyk cobordism, we prove that any smooth projective variety of Picard number 1, endowed with a $${\mathbb C}^*$$ C ∗ -action with only two fixed point components, induces a rooftop flip.