双重否定是最小否定

IF 0.7 3区数学 Q4 COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE

Journal of Logic Language and Information Pub Date : 2023-11-11 DOI:10.1007/s10849-023-09413-1

Satoru Niki

{"title":"双重否定是最小否定","authors":"Satoru Niki","doi":"10.1007/s10849-023-09413-1","DOIUrl":null,"url":null,"abstract":"Abstract N. Kamide introduced a pair of classical and constructive logics, each with a peculiar type of negation: its double negation behaves as classical and intuitionistic negation, respectively. A consequence of this is that the systems prove contradictions but are non-trivial. The present paper aims at giving insights into this phenomenon by investigating subsystems of Kamide’s logics, with a focus on a system in which the double negation behaves as the negation of minimal logic. We establish the negation inconsistency of the system and embeddability of contradictions from other systems. In addition, we attempt at an informational interpretation of the negation using the dimathematical framework of H. Wansing.","PeriodicalId":48732,"journal":{"name":"Journal of Logic Language and Information","volume":"16 7","pages":"0"},"PeriodicalIF":0.7000,"publicationDate":"2023-11-11","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Double Negation as Minimal Negation\",\"authors\":\"Satoru Niki\",\"doi\":\"10.1007/s10849-023-09413-1\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"Abstract N. Kamide introduced a pair of classical and constructive logics, each with a peculiar type of negation: its double negation behaves as classical and intuitionistic negation, respectively. A consequence of this is that the systems prove contradictions but are non-trivial. The present paper aims at giving insights into this phenomenon by investigating subsystems of Kamide’s logics, with a focus on a system in which the double negation behaves as the negation of minimal logic. We establish the negation inconsistency of the system and embeddability of contradictions from other systems. In addition, we attempt at an informational interpretation of the negation using the dimathematical framework of H. Wansing.\",\"PeriodicalId\":48732,\"journal\":{\"name\":\"Journal of Logic Language and Information\",\"volume\":\"16 7\",\"pages\":\"0\"},\"PeriodicalIF\":0.7000,\"publicationDate\":\"2023-11-11\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Logic Language and Information\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://doi.org/10.1007/s10849-023-09413-1\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Logic Language and Information","FirstCategoryId":"1085","ListUrlMain":"https://doi.org/10.1007/s10849-023-09413-1","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE","Score":null,"Total":0}

引用次数: 0

摘要

N. Kamide介绍了一对经典逻辑和建构逻辑，它们各自具有独特的否定类型:它们的双重否定分别表现为经典否定和直觉否定。这样做的一个后果是，这些系统证明了矛盾，但并非微不足道。本文旨在通过研究神出逻辑的子系统来深入了解这一现象，重点关注双重否定行为为最小逻辑否定的系统。建立了系统的否定性、矛盾性和其他系统矛盾的可嵌入性。此外，我们尝试使用万辛的数字框架对否定进行信息解释。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

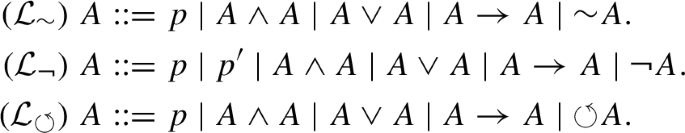
Double Negation as Minimal Negation

查看原文本刊更多论文

Double Negation as Minimal Negation

Abstract N. Kamide introduced a pair of classical and constructive logics, each with a peculiar type of negation: its double negation behaves as classical and intuitionistic negation, respectively. A consequence of this is that the systems prove contradictions but are non-trivial. The present paper aims at giving insights into this phenomenon by investigating subsystems of Kamide’s logics, with a focus on a system in which the double negation behaves as the negation of minimal logic. We establish the negation inconsistency of the system and embeddability of contradictions from other systems. In addition, we attempt at an informational interpretation of the negation using the dimathematical framework of H. Wansing.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Logic Language and Information COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCEL-LOGIC

CiteScore

1.70

自引率

12.50%

发文量

期刊介绍： The scope of the journal is the logical and computational foundations of natural, formal, and programming languages, as well as the different forms of human and mechanized inference. It covers the logical, linguistic, and information-theoretic parts of the cognitive sciences. Examples of main subareas are Intentional Logics including Dynamic Logic; Nonmonotonic Logic and Belief Revision; Constructive Logics; Complexity Issues in Logic and Linguistics; Theoretical Problems of Logic Programming and Resolution; Categorial Grammar and Type Theory; Generalized Quantification; Information-Oriented Theories of Semantic Structure like Situation Semantics, Discourse Representation Theory, and Dynamic Semantics; Connectionist Models of Logical and Linguistic Structures. The emphasis is on the theoretical aspects of these areas.