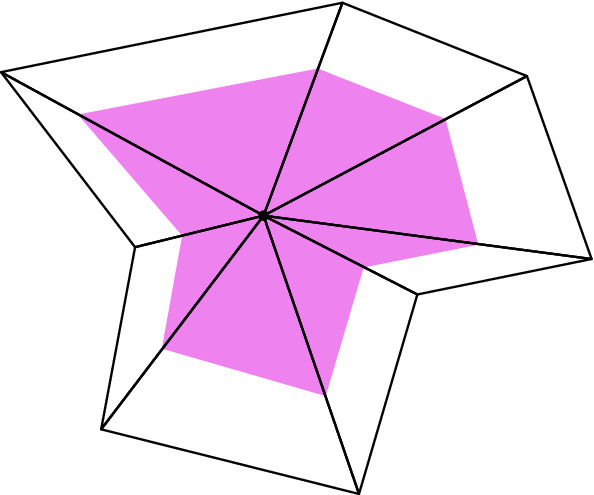
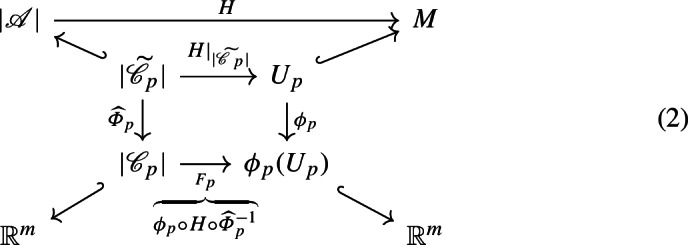
Local Criteria for Triangulating General Manifolds.

We present criteria for establishing a triangulation of a manifold. Given a manifold M, a simplicial complex  $A$ , and a map H from the underlying space of $A$ to M, our criteria are presented in local coordinate charts for M, and ensure that H is a homeomorphism. These criteria do not require a differentiable structure, or even an explicit metric on M. No Delaunay property of $A$ is assumed. The result provides a triangulation guarantee for algorithms that construct a simplicial complex by working in local coordinate patches. Because the criteria are easily verified in such a setting, they are expected to be of general use.