简约中的孤独点

IF 0.6 3区数学 Q4 COMPUTER SCIENCE, THEORY & METHODS

Discrete & Computational Geometry Pub Date : 2023-01-01 Epub Date: 2022-09-29 DOI:10.1007/s00454-022-00428-2

Maximilian Jaroschek, Manuel Kauers, Laura Kovács

{"title":"简约中的孤独点","authors":"Maximilian Jaroschek, Manuel Kauers, Laura Kovács","doi":"10.1007/s00454-022-00428-2","DOIUrl":null,"url":null,"abstract":"Given a lattice <math><mrow><mi>L</mi> <mo>⊆</mo> <msup><mi>Z</mi> <mi>m</mi></msup> </mrow> </math> and a subset <math><mrow><mi>A</mi> <mo>⊆</mo> <msup><mi>R</mi> <mi>m</mi></msup> </mrow> </math> , we say that a point in A is lonely if it is not equivalent modulo <math><mi>L</mi></math> to another point of A. We are interested in identifying lonely points for specific choices of <math><mi>L</mi></math> when A is a dilated standard simplex, and in conditions on <math><mi>L</mi></math> which ensure that the number of lonely points is unbounded as the simplex dilation goes to infinity.","PeriodicalId":50574,"journal":{"name":"Discrete & Computational Geometry","volume":"69 1","pages":"4-25"},"PeriodicalIF":0.6000,"publicationDate":"2023-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9805990/pdf/","citationCount":"0","resultStr":"{\"title\":\"Lonely Points in Simplices.\",\"authors\":\"Maximilian Jaroschek, Manuel Kauers, Laura Kovács\",\"doi\":\"10.1007/s00454-022-00428-2\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"Given a lattice <math><mrow><mi>L</mi> <mo>⊆</mo> <msup><mi>Z</mi> <mi>m</mi></msup> </mrow> </math> and a subset <math><mrow><mi>A</mi> <mo>⊆</mo> <msup><mi>R</mi> <mi>m</mi></msup> </mrow> </math> , we say that a point in A is lonely if it is not equivalent modulo <math><mi>L</mi></math> to another point of A. We are interested in identifying lonely points for specific choices of <math><mi>L</mi></math> when A is a dilated standard simplex, and in conditions on <math><mi>L</mi></math> which ensure that the number of lonely points is unbounded as the simplex dilation goes to infinity.\",\"PeriodicalId\":50574,\"journal\":{\"name\":\"Discrete & Computational Geometry\",\"volume\":\"69 1\",\"pages\":\"4-25\"},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2023-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9805990/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Discrete & Computational Geometry\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00454-022-00428-2\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"2022/9/29 0:00:00\",\"PubModel\":\"Epub\",\"JCR\":\"Q4\",\"JCRName\":\"COMPUTER SCIENCE, THEORY & METHODS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Discrete & Computational Geometry","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00454-022-00428-2","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"2022/9/29 0:00:00","PubModel":"Epub","JCR":"Q4","JCRName":"COMPUTER SCIENCE, THEORY & METHODS","Score":null,"Total":0}

引用次数: 0

摘要

给定一个网格 L ⊆ Z m 和一个子集 A ⊆ R m，如果 A 中的一个点不等价于 A 中的另一个点，那么我们就说这个点是孤点。我们感兴趣的是，当 A 是一个扩张的标准单纯形时，在 L 的特定选择下识别孤点，以及 L 的条件，这些条件可以确保孤点的数量在单纯形扩张到无穷大时是无限制的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

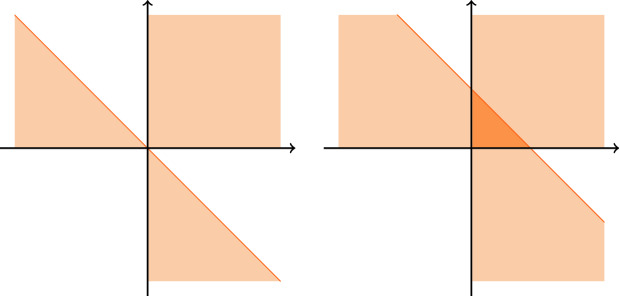
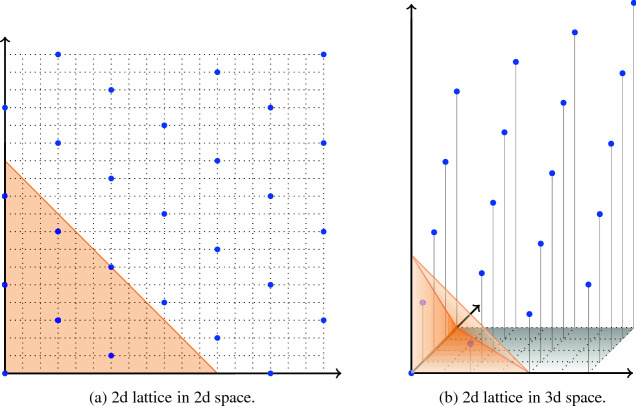
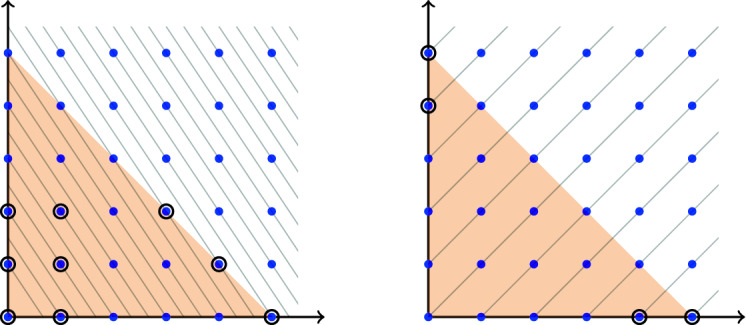
Lonely Points in Simplices.

查看原文本刊更多论文

Lonely Points in Simplices.

Given a lattice $L \subseteq Z^{m}$ and a subset $A \subseteq R^{m}$ , we say that a point in A is lonely if it is not equivalent modulo $L$ to another point of A. We are interested in identifying lonely points for specific choices of $L$ when A is a dilated standard simplex, and in conditions on $L$ which ensure that the number of lonely points is unbounded as the simplex dilation goes to infinity.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Discrete & Computational Geometry 数学-计算机：理论方法

CiteScore

1.80

自引率

12.50%

发文量

审稿时长

6-12 weeks

期刊介绍： Discrete & Computational Geometry (DCG) is an international journal of mathematics and computer science, covering a broad range of topics in which geometry plays a fundamental role. It publishes papers on such topics as configurations and arrangements, spatial subdivision, packing, covering, and tiling, geometric complexity, polytopes, point location, geometric probability, geometric range searching, combinatorial and computational topology, probabilistic techniques in computational geometry, geometric graphs, geometry of numbers, and motion planning.