具有整数创新的二元INMA模型的极大值问题。

IF 1 4区数学 Q3 STATISTICS & PROBABILITY

Methodology and Computing in Applied Probability Pub Date : 2022-01-01 DOI:10.1007/s11009-021-09920-3

J Hüsler, M G Temido, A Valente-Freitas

{"title":"具有整数创新的二元INMA模型的极大值问题。","authors":"J Hüsler, M G Temido, A Valente-Freitas","doi":"10.1007/s11009-021-09920-3","DOIUrl":null,"url":null,"abstract":"We study the limiting behaviour of the maximum of a bivariate (finite or infinite) moving average model, based on discrete random variables. We assume that the bivariate distribution of the iid innovations belong to the Anderson's class (Anderson, 1970). The innovations have an impact on the random variables of the INMA model by binomial thinning. We show that the limiting distribution of the bivariate maximum is also of Anderson's class, and that the components of the bivariate maximum are asymptotically independent.","PeriodicalId":18442,"journal":{"name":"Methodology and Computing in Applied Probability","volume":"24 4","pages":"2373-2402"},"PeriodicalIF":1.0000,"publicationDate":"2022-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC8852969/pdf/","citationCount":"0","resultStr":"{\"title\":\"On the Maximum of a Bivariate INMA Model with Integer Innovations.\",\"authors\":\"J Hüsler, M G Temido, A Valente-Freitas\",\"doi\":\"10.1007/s11009-021-09920-3\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We study the limiting behaviour of the maximum of a bivariate (finite or infinite) moving average model, based on discrete random variables. We assume that the bivariate distribution of the iid innovations belong to the Anderson's class (Anderson, 1970). The innovations have an impact on the random variables of the INMA model by binomial thinning. We show that the limiting distribution of the bivariate maximum is also of Anderson's class, and that the components of the bivariate maximum are asymptotically independent.\",\"PeriodicalId\":18442,\"journal\":{\"name\":\"Methodology and Computing in Applied Probability\",\"volume\":\"24 4\",\"pages\":\"2373-2402\"},\"PeriodicalIF\":1.0000,\"publicationDate\":\"2022-01-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC8852969/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Methodology and Computing in Applied Probability\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s11009-021-09920-3\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"STATISTICS & PROBABILITY\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Methodology and Computing in Applied Probability","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s11009-021-09920-3","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"STATISTICS & PROBABILITY","Score":null,"Total":0}

引用次数: 0

摘要

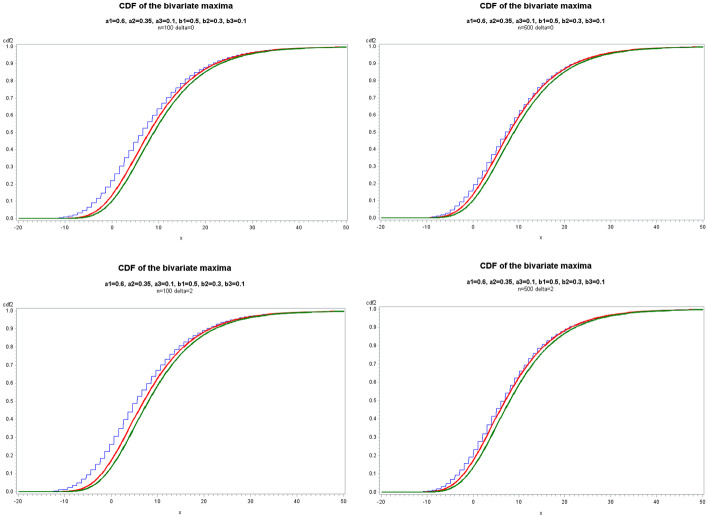
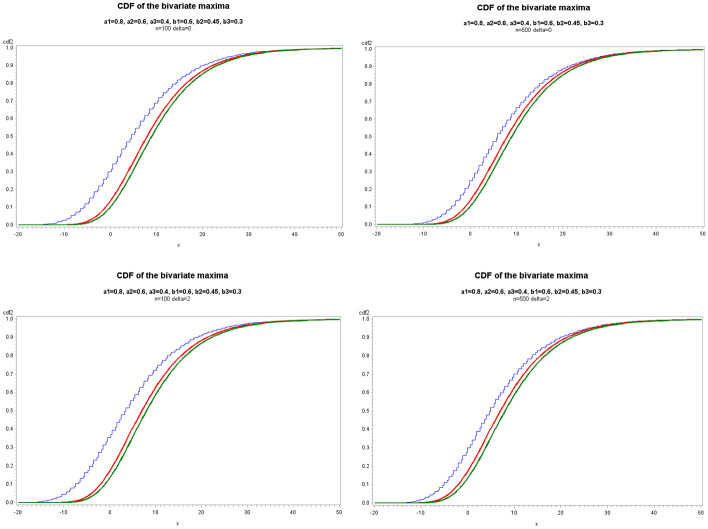
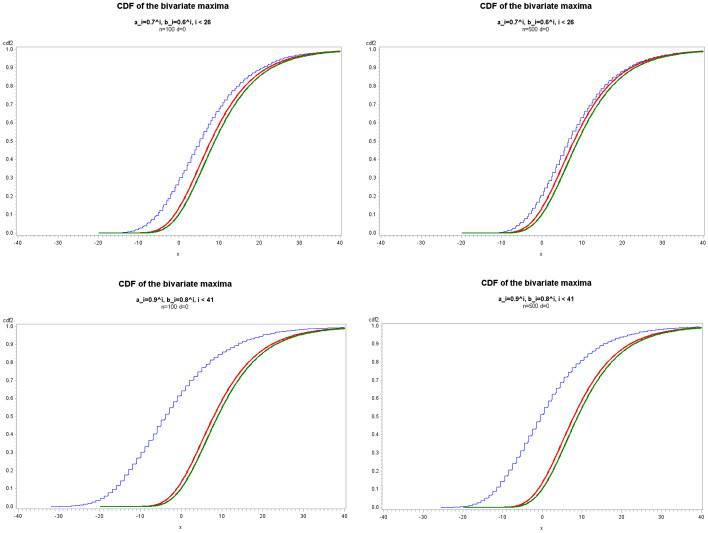
我们研究了基于离散随机变量的二元(有限或无限)移动平均模型的最大值的极限行为。我们假设iid创新的二元分布属于安德森类(Anderson, 1970)。这些创新通过二项细化对INMA模型的随机变量产生影响。我们证明了二元极大值的极限分布也属于Anderson类，并且二元极大值的分量是渐近独立的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

On the Maximum of a Bivariate INMA Model with Integer Innovations.

查看原文本刊更多论文

On the Maximum of a Bivariate INMA Model with Integer Innovations.

We study the limiting behaviour of the maximum of a bivariate (finite or infinite) moving average model, based on discrete random variables. We assume that the bivariate distribution of the iid innovations belong to the Anderson's class (Anderson, 1970). The innovations have an impact on the random variables of the INMA model by binomial thinning. We show that the limiting distribution of the bivariate maximum is also of Anderson's class, and that the components of the bivariate maximum are asymptotically independent.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Methodology and Computing in Applied Probability 数学-统计学与概率论

CiteScore

1.70

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： Methodology and Computing in Applied Probability will publish high quality research and review articles in the areas of applied probability that emphasize methodology and computing. Of special interest are articles in important areas of applications that include detailed case studies. Applied probability is a broad research area that is of interest to many scientists in diverse disciplines including: anthropology, biology, communication theory, economics, epidemiology, finance, linguistics, meteorology, operations research, psychology, quality control, reliability theory, sociology and statistics. The following alphabetical listing of topics of interest to the journal is not intended to be exclusive but to demonstrate the editorial policy of attracting papers which represent a broad range of interests: -Algorithms- Approximations- Asymptotic Approximations & Expansions- Combinatorial & Geometric Probability- Communication Networks- Extreme Value Theory- Finance- Image Analysis- Inequalities- Information Theory- Mathematical Physics- Molecular Biology- Monte Carlo Methods- Order Statistics- Queuing Theory- Reliability Theory- Stochastic Processes