On the Equilibrium of Elastic Bodies with a Weakly Curved Junction

Abstract

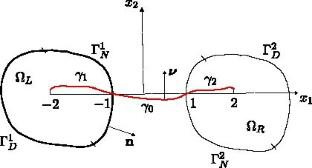
The paper addresses the analysis of a boundary value problem with an unknown contact area that describes equilibrium of two-dimensional elastic bodies with a thin weakly curved junction. It is assumed that the junction exfoliates from the elastic bodies to form interfacial cracks. Nonlinear boundary conditions in the form of inequalities are set on the crack faces and exclude the mutual penetration of the edges. The unique solvability of the boundary value problem is established. The analysis of passages to the limit as the junction stiffness parameter tends to infinity and to zero is carried out, and limit models are investigated.