Determining the Heat Flux Density in the Area of a Contact Line during the Evaporation of Liquid into a Bubble

Abstract

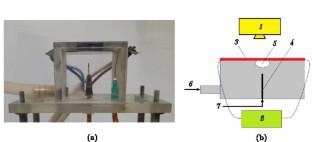
The article describes a method for determining the heat flux density on the surface of a thin foil that is inaccessible for thermal imaging measurements based on thermal imaging data on the other side of the foil, available for measurements. Mathematically, the problem is reduced to solving the Cauchy problem for an elliptic equation, which is ill-posed. The problem is solved using noise smoothing in the initial temperature field and a correct restriction on the number of expansion terms in the Fourier series. According to the measurement results, the heat flux density reaches its maximum in the area of the contact line and amounts to \( 4200~\text {W}/\text {m}^2 \).