Semifinite Harmonic Functions on the Zigzag Graph
IF 0.7
4区 数学
Q3 MATHEMATICS
引用次数: 2
Abstract
We study semifinite harmonic functions on the zigzag graph, which corresponds to the Pieri rule for the fundamental quasisymmetric functions \(\{F_{\lambda}\}\). The main problem, which we solve here, is to classify the indecomposable semifinite harmonic functions on this graph. We show that these functions are in a natural bijective correspondence with some combinatorial data, the so-called semifinite zigzag growth models. Furthermore, we describe an explicit construction that produces a semifinite indecomposable harmonic function from every semifinite zigzag growth model. We also establish a semifinite analogue of the Vershik–Kerov ring theorem.
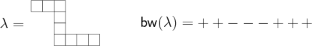
z形图上的半有限调和函数
我们研究了之字形图上的半有限调和函数,它对应于基本拟对称函数\(\{F_{\lambda}\}\)的Pieri规则。我们在这里要解决的主要问题是对这个图上不可分解的半有限调和函数进行分类。我们证明了这些函数与一些组合数据,即所谓的半有限之字形增长模型,具有自然的双射对应关系。进一步地,我们描述了从每一个半有限之字形增长模型产生一个半有限不可分解调和函数的显式构造。我们还建立了Vershik-Kerov环定理的半有限类似。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
0.90
自引率
0.00%
发文量
7
审稿时长
>12 weeks
期刊介绍:
Functional Analysis and Its Applications publishes current problems of functional analysis, including representation theory, theory of abstract and functional spaces, theory of operators, spectral theory, theory of operator equations, and the theory of normed rings. The journal also covers the most important applications of functional analysis in mathematics, mechanics, and theoretical physics.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


