Well-posedness and decay in a system of hyperbolic and biharmonic-wave equations with variable exponents and weak dampings

IF 0.9 Q2 MATHEMATICS

Arabian Journal of Mathematics Pub Date : 2023-05-30 DOI:10.1007/s40065-023-00431-2

Oulia Bouhoufani

引用次数: 0

Abstract

In this paper, we consider a coupled system of hyperbolic and biharmonic-wave equations with variable exponents in the damping and coupling terms. In each equation, the damping term is modulated by a time-dependent coefficient a(t) (or b(t)). First, we state and prove a well-posedness theorem of global weak solutions, by exploiting Galerkin’s method and some compactness arguments. Then, using the multiplier method, we establish the decay rates of the solution energy, under suitable assumptions on the time-dependent coefficients and the range of the variable exponents. We end our work with some illustrative examples.

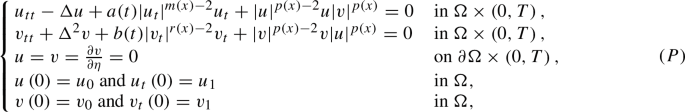
Abstract Image

查看原文本刊更多论文

变指数弱阻尼双曲和双调和波动方程组的适定性和衰变

在本文中，我们考虑了一个在阻尼项和耦合项中具有变指数的双曲和二次谐波方程的耦合系统。在每个方程中，阻尼项由时间相关系数a（t）（或b（t））调制。首先，利用Galerkin方法和一些紧致性论证，给出并证明了全局弱解的适定性定理。然后，使用乘法器方法，在适当的时间相关系数和可变指数范围的假设下，我们建立了解能量的衰减率。我们以一些说明性的例子结束我们的工作。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Arabian Journal of Mathematics MATHEMATICS-

CiteScore

2.20

自引率

8.30%

发文量

审稿时长

13 weeks

期刊介绍： The Arabian Journal of Mathematics is a quarterly, peer-reviewed open access journal published under the SpringerOpen brand, covering all mainstream branches of pure and applied mathematics. Owned by King Fahd University of Petroleum and Minerals, AJM publishes carefully refereed research papers in all main-stream branches of pure and applied mathematics. Survey papers may be submitted for publication by invitation only.To be published in AJM, a paper should be a significant contribution to the mathematics literature, well-written, and of interest to a wide audience. All manuscripts will undergo a strict refereeing process; acceptance for publication is based on two positive reviews from experts in the field.Submission of a manuscript acknowledges that the manuscript is original and is not, in whole or in part, published or submitted for publication elsewhere. A copyright agreement is required before the publication of the paper.Manuscripts must be written in English. It is the author''s responsibility to make sure her/his manuscript is written in clear, unambiguous and grammatically correct language.