Solution to the n-bubble problem on \(\mathbb {R}^1\) with log-concave density
IF 0.7
3区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
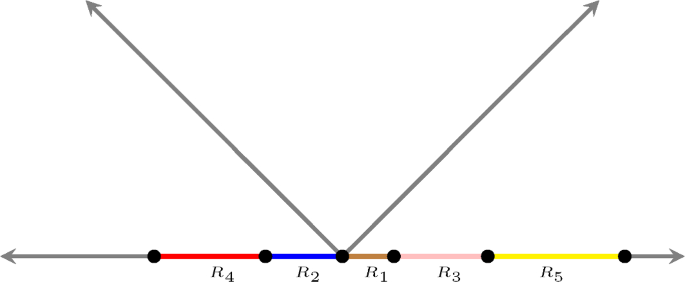
We study the n-bubble problem on \(\mathbb {R}^1\) with a prescribed density function f that is even, radially increasing, and satisfies a log-concavity requirement. Under these conditions, we find that isoperimetric solutions can be identified for an arbitrary number of regions, and that these solutions have a well-understood and regular structure. This generalizes recent work done on the density function \(|x |^p\) and stands in contrast to log-convex density functions which are known to have no such regular structure.
具有对数凹密度的\(\mathbb{R}^1)上n气泡问题的解
我们研究了具有规定密度函数f的\(\mathbb{R}^1)上的n气泡问题,该密度函数f是均匀的、径向递增的,并且满足对数凹度要求。在这些条件下,我们发现对于任意数量的区域,等周解可以被识别,并且这些解具有被充分理解的规则结构。这推广了最近关于密度函数(|x|^p\)的工作,并与已知没有这种正则结构的对数凸密度函数形成了对比。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.20
自引率
0.00%
发文量
70
审稿时长
6-12 weeks
期刊介绍:
This journal examines global problems of geometry and analysis as well as the interactions between these fields and their application to problems of theoretical physics. It contributes to an enlargement of the international exchange of research results in the field.
The areas covered in Annals of Global Analysis and Geometry include: global analysis, differential geometry, complex manifolds and related results from complex analysis and algebraic geometry, Lie groups, Lie transformation groups and harmonic analysis, variational calculus, applications of differential geometry and global analysis to problems of theoretical physics.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


