Relatively Maximal Subgroups of Odd Index in Symmetric Groups
IF 0.4
3区 数学
Q4 LOGIC
引用次数: 0
Abstract
Let 𝖃 be a class of finite groups which contains a group of order 2 and is closed under subgroups, homomorphic images, and extensions. We define the concept of an 𝖃-admissible diagram representing a natural number n. Associated with each n are finitely many such diagrams, and they all can be found easily. Admissible diagrams representing a number n are used to uniquely parametrize conjugacy classes of maximal 𝖃-subgroups of odd index in the symmetric group Symn, and we define the structure of such groups. As a consequence, we obtain a complete classification of submaximal 𝖃-subgroups of odd index in alternating groups.
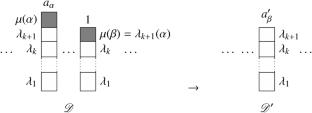
对称群中奇指数的相对极大子群
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Algebra and Logic
数学-数学
CiteScore
1.10
自引率
20.00%
发文量
26
审稿时长
>12 weeks
期刊介绍:
This bimonthly journal publishes results of the latest research in the areas of modern general algebra and of logic considered primarily from an algebraic viewpoint. The algebraic papers, constituting the major part of the contents, are concerned with studies in such fields as ordered, almost torsion-free, nilpotent, and metabelian groups; isomorphism rings; Lie algebras; Frattini subgroups; and clusters of algebras. In the area of logic, the periodical covers such topics as hierarchical sets, logical automata, and recursive functions.
Algebra and Logic is a translation of ALGEBRA I LOGIKA, a publication of the Siberian Fund for Algebra and Logic and the Institute of Mathematics of the Siberian Branch of the Russian Academy of Sciences.
All articles are peer-reviewed.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


