Global existence and asymptotic behavior for a Timoshenko system with internal damping and logarithmic source terms

IF 0.9 Q2 MATHEMATICS

Arabian Journal of Mathematics Pub Date : 2022-12-12 DOI:10.1007/s40065-022-00411-y

Sebastião Martins Siqueira Cordeiro, Ducival Carvalho Pereira, Carlos Alessandro da Costa Baldez, Carlos Alberto Raposo da Cunha

引用次数: 1

Abstract

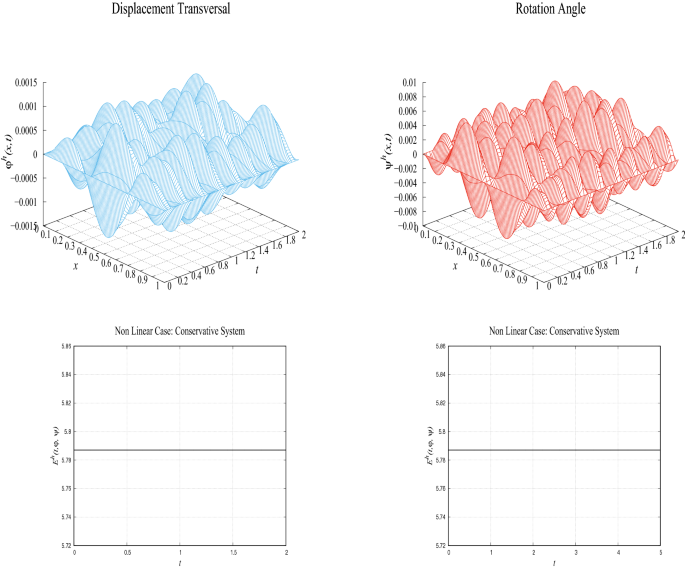
This manuscript deals with a Timoshenko system with damping and source. The existence and stability of the solution are analyzed taking into account the competition of the internal damping versus the logarithmic source. We use the potential well theory. For initial data in the stability set created by the Nehari surface, the existence of global solutions is proved using Faedo–Galerkin’s approximation. The exponential decay is given by the Nakao theorem. A numerical approach is presented to illustrate the results obtained.

Abstract Image

查看原文本刊更多论文

具有内阻尼和对数源项的Timoshenko系统的全局存在性和渐近性

本文研究了一个具有阻尼和源的Timoshenko系统。考虑到内部阻尼与对数源的竞争，分析了解的存在性和稳定性。我们使用势阱理论。对于由Nehari曲面创建的稳定性集中的初始数据，使用Faedo–Galerkin近似证明了全局解的存在性。指数衰减是由Nakao定理给出的。给出了一种数值方法来说明所获得的结果。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Arabian Journal of Mathematics MATHEMATICS-

CiteScore

2.20

自引率

8.30%

发文量

审稿时长

13 weeks

期刊介绍： The Arabian Journal of Mathematics is a quarterly, peer-reviewed open access journal published under the SpringerOpen brand, covering all mainstream branches of pure and applied mathematics. Owned by King Fahd University of Petroleum and Minerals, AJM publishes carefully refereed research papers in all main-stream branches of pure and applied mathematics. Survey papers may be submitted for publication by invitation only.To be published in AJM, a paper should be a significant contribution to the mathematics literature, well-written, and of interest to a wide audience. All manuscripts will undergo a strict refereeing process; acceptance for publication is based on two positive reviews from experts in the field.Submission of a manuscript acknowledges that the manuscript is original and is not, in whole or in part, published or submitted for publication elsewhere. A copyright agreement is required before the publication of the paper.Manuscripts must be written in English. It is the author''s responsibility to make sure her/his manuscript is written in clear, unambiguous and grammatically correct language.