Wiener–Hopf technique for a fractional mixed boundary value problem in cylindrical layer

IF 0.9 Q2 MATHEMATICS

Arabian Journal of Mathematics Pub Date : 2023-07-07 DOI:10.1007/s40065-023-00437-w

Alireza Ansari, Mohammad Rasool Masomi

引用次数: 0

Abstract

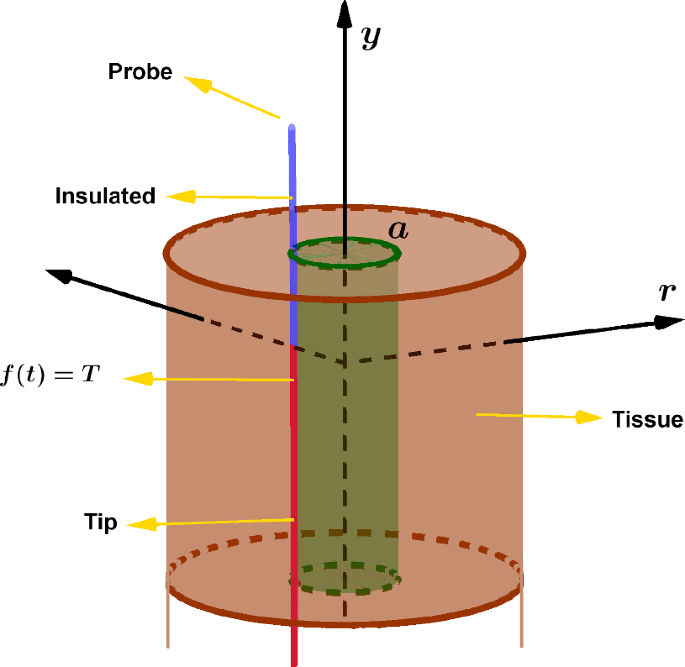
In this paper, we study the heat transfer modeling during freezing of a biological tissue and present an analytical approach for solving the heat transfer problem in cryosurgery. We consider a time-fractional bio-heat equation in the cylindrical coordinate and employ the Wiener–Hopf technique to find the temperature of tissue in two different domains by the factorization of associated Wiener–Hopf kernel. We discuss the fundamental roles of the Bessel and Wright functions in determining the analytical solution of fractional cryosurgery problem.

Abstract Image

查看原文本刊更多论文

圆柱层中分数混合边值问题的Wiener-Hopf技术

在本文中，我们研究了生物组织冷冻过程中的传热建模，并提出了一种解决冷冻手术中传热问题的分析方法。我们考虑圆柱坐标系中的时间分数阶生物热方程，并采用维纳-霍普夫技术，通过相关维纳-霍普f核的因子分解，找到两个不同区域中组织的温度。我们讨论了贝塞尔函数和莱特函数在确定分数冷冻手术问题解析解中的基本作用。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Arabian Journal of Mathematics MATHEMATICS-

CiteScore

2.20

自引率

8.30%

发文量

审稿时长

13 weeks

期刊介绍： The Arabian Journal of Mathematics is a quarterly, peer-reviewed open access journal published under the SpringerOpen brand, covering all mainstream branches of pure and applied mathematics. Owned by King Fahd University of Petroleum and Minerals, AJM publishes carefully refereed research papers in all main-stream branches of pure and applied mathematics. Survey papers may be submitted for publication by invitation only.To be published in AJM, a paper should be a significant contribution to the mathematics literature, well-written, and of interest to a wide audience. All manuscripts will undergo a strict refereeing process; acceptance for publication is based on two positive reviews from experts in the field.Submission of a manuscript acknowledges that the manuscript is original and is not, in whole or in part, published or submitted for publication elsewhere. A copyright agreement is required before the publication of the paper.Manuscripts must be written in English. It is the author''s responsibility to make sure her/his manuscript is written in clear, unambiguous and grammatically correct language.