Estimation of \( P[Y Q1 Decision Sciences Annals of Data Science Pub Date : 2023-08-17 DOI:10.1007/s40745-023-00487-z Dipak D. Patil, U. V. Naik-Nimbalkar, M. M. Kale 求助PDF {"title":"Estimation of \\( P[Y<X] \\) for Dependence of Stress–Strength Models with Weibull Marginals","authors":"Dipak D. Patil,&nbsp;U. V. Naik-Nimbalkar,&nbsp;M. M. Kale","doi":"10.1007/s40745-023-00487-z","DOIUrl":null,"url":null,"abstract":"<div><p>The stress–strength model is a basic tool used in evaluating the reliability <span>\\( R = P(Y &lt; X)\\)</span>. We consider an expression for <i>R</i> where the random variables X and Y denote strength and stress, respectively. The system fails only if the stress exceeds the strength. We aim to study the effect of the dependency between X and Y on <i>R</i>. We assume that X and Y follow Weibull distributions and their dependency is modeled by a copula with the dependency parameter <span>\\( \\theta \\)</span>. We compute <i>R</i> for Farlie–Gumbel–Morgenstern (FGM), Ali–Mikhail–Haq (AMH), Gumbel’s bivariate exponential copulas, and for Gumbel–Hougaard (GH) copula using a Monte-Carlo integration technique. We plot the graph of <i>R</i> versus <span>\\(\\theta \\)</span> to study the effect of dependency on <i>R</i>. We estimate <i>R</i> by plugging in the estimates of the marginal parameters and of <span>\\( \\theta \\)</span> in its expression. The estimates of the marginal parameters are based on the marginal likelihood. The estimates of <span>\\(\\theta \\)</span> are obtained from two different methods; one is based on the conditional likelihood and the other is based on the method of moments using Blomqvist’s beta. Asymptotic distribution of both the estimators of <i>R</i> is obtained. Finally, analysis of real data set is also performed for illustrative purposes.</p></div>","PeriodicalId":36280,"journal":{"name":"Annals of Data Science","volume":null,"pages":null},"PeriodicalIF":0.0000,"publicationDate":"2023-08-17","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Annals of Data Science","FirstCategoryId":"1085","ListUrlMain":"https://link.springer.com/article/10.1007/s40745-023-00487-z","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"Decision Sciences","Score":null,"Total":0} 引用次数: 0 引用 批量引用 Abstract 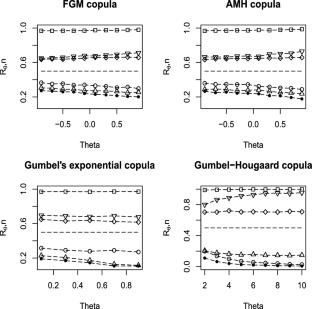The stress–strength model is a basic tool used in evaluating the reliability \( R = P(Y < X)\). We consider an expression for R where the random variables X and Y denote strength and stress, respectively. The system fails only if the stress exceeds the strength. We aim to study the effect of the dependency between X and Y on R. We assume that X and Y follow Weibull distributions and their dependency is modeled by a copula with the dependency parameter \( \theta \). We compute R for Farlie–Gumbel–Morgenstern (FGM), Ali–Mikhail–Haq (AMH), Gumbel’s bivariate exponential copulas, and for Gumbel–Hougaard (GH) copula using a Monte-Carlo integration technique. We plot the graph of R versus \(\theta \) to study the effect of dependency on R. We estimate R by plugging in the estimates of the marginal parameters and of \( \theta \) in its expression. The estimates of the marginal parameters are based on the marginal likelihood. The estimates of \(\theta \) are obtained from two different methods; one is based on the conditional likelihood and the other is based on the method of moments using Blomqvist’s beta. Asymptotic distribution of both the estimators of R is obtained. Finally, analysis of real data set is also performed for illustrative purposes. 分享 查看原文 本刊更多论文 具有威布尔边际的应力-强度模型依赖性的$$P[Y 应力-强度模型是用于评估可靠性的基本工具（R = P(Y < X)）。我们考虑 R 的表达式，其中随机变量 X 和 Y 分别表示强度和应力。只有当应力超过强度时，系统才会失效。我们假定 X 和 Y 遵循 Weibull 分布，它们之间的依赖关系由具有依赖参数 \( \theta \)的 copula 来建模。我们使用蒙特卡洛积分技术计算 Farlie-Gumbel-Morgenstern (FGM)、Ali-Mikhail-Haq (AMH)、Gumbel 的双变量指数协程以及 Gumbel-Hougaard (GH) 协程的 R。我们绘制了 R 与 \(\theta \)的关系图，以研究依赖性对 R 的影响。我们在 R 的表达式中插入边际参数和 \(\theta \)的估计值来估计 R。边际参数的估计基于边际似然法。\(\theta \)的估计值由两种不同的方法获得；一种是基于条件似然法，另一种是基于使用布隆奎斯特贝塔的矩方法。两种 R 估计数的渐近分布都已得到。最后，还对真实数据集进行了分析，以说明问题。 本文章由计算机程序翻译，如有差异，请以英文原文为准。 求助全文 约1分钟内获得全文 求助全文 来源期刊 Annals of Data Science Decision Sciences-Statistics, Probability and Uncertainty CiteScore 6.50 自引率 0.00% 发文量 93 期刊介绍： Annals of Data Science (ADS) publishes cutting-edge research findings, experimental results and case studies of data science. Although Data Science is regarded as an interdisciplinary field of using mathematics, statistics, databases, data mining, high-performance computing, knowledge management and virtualization to discover knowledge from Big Data, it should have its own scientific contents, such as axioms, laws and rules, which are fundamentally important for experts in different fields to explore their own interests from Big Data. ADS encourages contributors to address such challenging problems at this exchange platform. At present, how to discover knowledge from heterogeneous data under Big Data environment needs to be addressed. ADS is a series of volumes edited by either the editorial office or guest editors. Guest editors will be responsible for call-for-papers and the review process for high-quality contributions in their volumes. 相关文献 × 引用 GB/T 7714-2015 复制 MLA 复制 APA 复制 导出至 BibTeX EndNote RefMan NoteFirst NoteExpress × 求助内容： 期刊论文 学位论文 图书 其他 (专利、报告等) 只需要正文 仅需补充材料 应助结果提醒方式： 微信（请自行确认已关注Book学术公众号） 邮件 保存 保存后同步修改账户信息中的邮箱 确认发布求助 × 处理提示 您的部分求助已有人上传文件，您还尚未处理，请先处理完毕再发起新的求助 点击查看 × 努力提交中 提交成功 继续求助查看详情 × 提示 您的信息不完整，为了账户安全，请先补充。 现在去补充 × 没积分了 多种获得积分方式，供你选择！ 查看如何获取积分 × 提示 您因"违规操作" 具体请查看互助需知 我知道了 × 提示 现在去查看 取消 × 提示 确定 × 快捷登录 密码登录 用户名： 密码： 验证码： 两周内记住我 忘记密码？ 手机号： 验证码： 没有帐号？现在注册 请完成安全验证× 微信好友 朋友圈 QQ好友 复制链接 取消 已复制链接 快去分享给好友吧! 我知道了 点击右上角分享 0 $(function () { var title = $("#title").val(); var id = $("#id").val(); $.post("/Literature/GetRelatedLiterature", { id: id, title: title }, function (result) { if (result != null) { var html = ``; for (var i = 0; i < result.length; i++) { html += `<div class="sslist">`; html += `<a class="caption" href="` + $("#url1").val() + result[i].ArticleID + `.htm">` + result[i].Title + `</a>`; html += ` <div class="substance">`; html += `<span class="IF">IF ` + result[i].PeriodicalIF + ` </span>`; if (result[i].RegionNum > 0) { html += `<span class="fq` + result[i].RegionNum + `">` + result[i].RegionNum + `区 ` + result[i].RegionCategory + `</span>`; } //var EmployDataBaseShoreName = result[i].EmployDataBaseShoreName; //if (EmployDataBaseShoreName != "" && EmployDataBaseShoreName!=null) { // var names = EmployDataBaseShoreName.split('||') // for (var j = 0; j < names.length; j++) { // html += `<span class="fq5">` + names[j] + `</span>`; // } //} //html += ``; html += `</div>`; html += `<div class="substance">`; html += `<a href="` + $("#url2").val() + "_d" + result[i].PeriodicalID + `.htm" target="_blank">` + result[i].PeriodicalName + `</a>`; html += `<span class="Pub">Pub Date : ` + result[i].PublishDate + `</span>`; html += `</div>`; html += ` <div class="author">`; html += result[i].AuthorName; html += `</div>`; html += `</div>`; } if (html.length > 0) { $("#xglist").show(); $("#xglist").append(html); } } }); getReferenceCount(); }); function getReferenceCount() { var LocalId = localStorage.getItem("referenceName"); if (LocalId != null) { $.get("/Literature/GetBatchReferenceCountByLocalId", { LocalId: LocalId }, function (result) { $("#referencecount").html(result.Code); }, "json"); } else { $("#referencecount").html('0'); } } wx.config({ debug: false, appId: 'wx999b2eb01732df2e', timestamp: '1732038739', nonceStr: 'fORtYoAQTnb8om3e', signature: '0f7479cf6abae576a5fc451040308c8634b14ec3', jsApiList: [ 'onMenuShareTimeline', 'onMenuShareAppMessage', 'hideMenuItems' ] });

Abstract

The stress–strength model is a basic tool used in evaluating the reliability \( R = P(Y < X)\). We consider an expression for R where the random variables X and Y denote strength and stress, respectively. The system fails only if the stress exceeds the strength. We aim to study the effect of the dependency between X and Y on R. We assume that X and Y follow Weibull distributions and their dependency is modeled by a copula with the dependency parameter \( \theta \). We compute R for Farlie–Gumbel–Morgenstern (FGM), Ali–Mikhail–Haq (AMH), Gumbel’s bivariate exponential copulas, and for Gumbel–Hougaard (GH) copula using a Monte-Carlo integration technique. We plot the graph of R versus \(\theta \) to study the effect of dependency on R. We estimate R by plugging in the estimates of the marginal parameters and of \( \theta \) in its expression. The estimates of the marginal parameters are based on the marginal likelihood. The estimates of \(\theta \) are obtained from two different methods; one is based on the conditional likelihood and the other is based on the method of moments using Blomqvist’s beta. Asymptotic distribution of both the estimators of R is obtained. Finally, analysis of real data set is also performed for illustrative purposes.