Model category of diffeological spaces
IF 0.5
4区 数学
引用次数: 17
Abstract
The existence of a model structure on the category \({\mathcal {D}}\) of diffeological spaces is crucial to developing smooth homotopy theory. We construct a compactly generated model structure on the category \({\mathcal {D}}\) whose weak equivalences are just smooth maps inducing isomorphisms on smooth homotopy groups. The essential part of our construction of the model structure on \({\mathcal {D}}\) is to introduce diffeologies on the sets \(\varDelta ^{p}\)\((p \ge 0)\) such that \(\varDelta ^{p}\) contains the \(k\mathrm{th}\) horn \(\varLambda ^{p}_{k}\) as a smooth deformation retract.
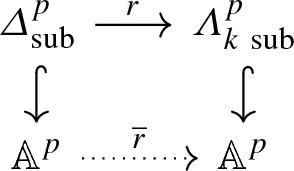
微分空间的模型范畴
在微分空间的\({\mathcal {D}}\)范畴上模型结构的存在性对于发展光滑同伦理论是至关重要的。我们在范畴\({\mathcal {D}}\)上构造了一个紧生成的模型结构,其弱等价是光滑同伦群上诱导同构的光滑映射。我们在\({\mathcal {D}}\)上构建模型结构的关键部分是在\(\varDelta ^{p}\)\((p \ge 0)\)上引入差分,使\(\varDelta ^{p}\)包含\(k\mathrm{th}\)角\(\varLambda ^{p}_{k}\)作为平滑变形缩回。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Homotopy and Related Structures
Mathematics-Geometry and Topology
自引率
0.00%
发文量
0
期刊介绍:
Journal of Homotopy and Related Structures (JHRS) is a fully refereed international journal dealing with homotopy and related structures of mathematical and physical sciences.
Journal of Homotopy and Related Structures is intended to publish papers on
Homotopy in the broad sense and its related areas like Homological and homotopical algebra, K-theory, topology of manifolds, geometric and categorical structures, homology theories, topological groups and algebras, stable homotopy theory, group actions, algebraic varieties, category theory, cobordism theory, controlled topology, noncommutative geometry, motivic cohomology, differential topology, algebraic geometry.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


