Lagrangian cobordism functor in microlocal sheaf theory I
IF 1.1
2区 数学
Q2 MATHEMATICS
引用次数: 5
Abstract
Let be Legendrian submanifolds in the cosphere bundle . Given a Lagrangian cobordism of Legendrians from to , we construct a functor between sheaf categories of compact objects with singular support on and its right adjoint on sheaf categories of proper objects, using Nadler–Shende's work. This gives a sheaf theory description analogous to the Lagrangian cobordism map on Legendrian contact homologies and the right adjoint on their unital augmentation categories. We also deduce some long exact sequences and new obstructions to Lagrangian cobordisms between high-dimensional Legendrian submanifolds.
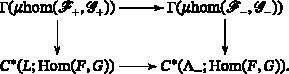
微局部簇理论I中的拉格朗日共基函子
让Λ±$\Lambda _\pm$ 是球束T *,∞M中的legend子流形$T^{*,\infty }M$ . 给定拉格朗日坐标L$L$ 来自Λ−$\Lambda _-$ 到Λ+$\Lambda _+$ ,构造了一个函子ΦL*:ShΛ+c(M)→ShΛ−c(M)⊗c−*(Ω*Λ−)c−*(Ω*L)${\mathrm{\Phi}}_{L}^{\ast}:{{\rm Sh}}_{{\mathrm{\Lambda}}_{+}}^{c}(M)\to {{\rm Sh}}_{{\mathrm{\Lambda}}_{-}}^{c}(M){\otimes}_{{C}_{-\ast}({\mathrm{\Omega}}_{\ast}{\mathrm{\Lambda}}_{-})}{C}_{-\ast}({\mathrm{\Omega}}_{\ast}L)$ 在Λ±上具有奇异支持的紧凑物体的轴类之间$\Lambda _\pm$ 以及它在固有对象的一组范畴上的右伴随,使用了Nadler-Shende的工作。这给出了一个类似于Legendrian接触同调上的拉格朗日协同映射及其单位增广范畴上的右伴随的束理论描述。我们还推导出了高维legendsub流形之间拉格朗日协同的一些长精确序列和新的障碍。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Topology
数学-数学
CiteScore
2.00
自引率
9.10%
发文量
62
审稿时长
>12 weeks
期刊介绍:
The Journal of Topology publishes papers of high quality and significance in topology, geometry and adjacent areas of mathematics. Interesting, important and often unexpected links connect topology and geometry with many other parts of mathematics, and the editors welcome submissions on exciting new advances concerning such links, as well as those in the core subject areas of the journal.
The Journal of Topology was founded in 2008. It is published quarterly with articles published individually online prior to appearing in a printed issue.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


