Smashing localizations in equivariant stable homotopy

Abstract

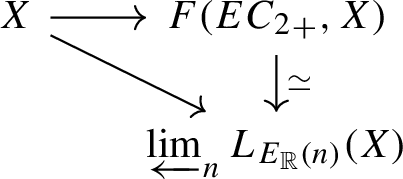
We study how smashing Bousfield localizations behave under various equivariant functors. We show that the analogs of the smash product and chromatic convergence theorems for the Real Johnson–Wilson theories \(E_{\mathbb {R}}(n)\) hold only after Borel completion. We establish analogous results for the \(C_{2^n}\)-equivariant Johnson–Wilson theories constructed by Beaudry, Hill, Shi, and Zeng. We show that induced localizations upgrade the available norms for an \(N_\infty \)-algebra, and we determine which new norms appear. Finally, we explore generalizations of our results on smashing localizations in the context of a quasi-Galois extension of \(E_\infty \)-rings.