Displacement Discontinuity Method Taking into Account the Curvature of the Crack

Abstract

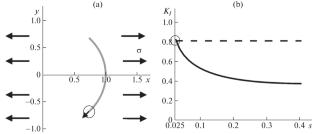
The paper is devoted to the development of the displacement discontinuity method for plane problems of fracture mechanics in consideration of the curvature of crack lines. In this paper, some new representations of biharmonic functions are found. This is necessary to obtain the analytical solutions of problems for an elastic plane weakened by a crack in the form of a circular arc. A numerical method is proposed on the basis of these analytical solutions. The numerical values of the stress intensity factor are compared with its known analytical value.