Growing Random Uniform d-ary Trees
IF 0.6
4区 数学
Q4 MATHEMATICS, APPLIED
引用次数: 4
Abstract
Let \({{\mathcal {T}}}_{d}(n)\) be the set of d-ary rooted trees with n internal nodes. We give a method to construct a sequence \(( \textbf{t}_{n},n\ge 0)\), where, for any \(n\ge 1\), \( \textbf{t}_{n}\) has the uniform distribution in \({{\mathcal {T}}}_{d}(n)\), and \( \textbf{t}_{n}\) is constructed from \( \textbf{t}_{n-1}\) by the addition of a new node, and a rearrangement of the structure of \( \textbf{t}_{n-1}\). This method is inspired by Rémy’s algorithm which does this job in the binary case, but it is different from it. This provides a method for the random generation of a uniform d-ary tree in \({{\mathcal {T}}}_{d}(n)\) with a cost linear in n.
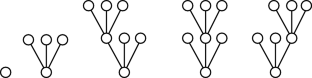
生长随机均匀树
设\({{\mathcal{T}}_{d}(n)\)是具有n个内部节点的d元根树的集合。我们给出了一个构造序列\(\textbf{t}_{n} ,n\ge 0)\),其中,对于任何\(n\ge 1\),\(\textbf{t}_{n} \)在\({\mathcal{T}}_{d}(n)\)和\(\textbf)中具有均匀分布{t}_{n} \)由\(\textbf)构造{t}_{n-1}\),添加一个新节点,并重新排列\(\textbf)的结构{t}_{n-1}\)。该方法的灵感来自Rémy的算法,该算法在二进制情况下完成这项工作,但与之不同。这提供了一种随机生成\({\mathcal{T}}}_{d}(n)\)中成本线性的一致d元树的方法。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Annals of Combinatorics
数学-应用数学
CiteScore
1.00
自引率
0.00%
发文量
56
审稿时长
>12 weeks
期刊介绍:
Annals of Combinatorics publishes outstanding contributions to combinatorics with a particular focus on algebraic and analytic combinatorics, as well as the areas of graph and matroid theory. Special regard will be given to new developments and topics of current interest to the community represented by our editorial board.
The scope of Annals of Combinatorics is covered by the following three tracks:
Algebraic Combinatorics:
Enumerative combinatorics, symmetric functions, Schubert calculus / Combinatorial Hopf algebras, cluster algebras, Lie algebras, root systems, Coxeter groups / Discrete geometry, tropical geometry / Discrete dynamical systems / Posets and lattices
Analytic and Algorithmic Combinatorics:
Asymptotic analysis of counting sequences / Bijective combinatorics / Univariate and multivariable singularity analysis / Combinatorics and differential equations / Resolution of hard combinatorial problems by making essential use of computers / Advanced methods for evaluating counting sequences or combinatorial constants / Complexity and decidability aspects of combinatorial sequences / Combinatorial aspects of the analysis of algorithms
Graphs and Matroids:
Structural graph theory, graph minors, graph sparsity, decompositions and colorings / Planar graphs and topological graph theory, geometric representations of graphs / Directed graphs, posets / Metric graph theory / Spectral and algebraic graph theory / Random graphs, extremal graph theory / Matroids, oriented matroids, matroid minors / Algorithmic approaches
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


