The n-fold reduced bar construction
IF 0.5
4区 数学
引用次数: 1
Abstract
This paper is about a correspondence between monoidal structures in categories and n-fold loop spaces. We developed a new syntactical technique whose role is to substitute the coherence results, which were the main ingredients in the proof that the Segal–Thomason bar construction provides an appropriate simplicial space. The results we present here enable more common categories to enter this delooping machine. For example, such as the category of finite sets with two monoidal structures brought by the disjoint union and Cartesian product.
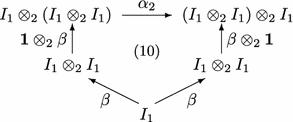
n倍减杆结构
本文研究了范畴中单形结构与n重环空间的对应关系。我们开发了一种新的句法技术,其作用是代替相干结果,相干结果是证明Segal-Thomason条结构提供适当的简单空间的主要成分。我们在这里提出的结果使更多的常见类别能够进入这台正在发展的机器。例如,由不相交并和笛卡尔积所带来的具有两个单形结构的有限集的范畴。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Homotopy and Related Structures
Mathematics-Geometry and Topology
自引率
0.00%
发文量
0
期刊介绍:
Journal of Homotopy and Related Structures (JHRS) is a fully refereed international journal dealing with homotopy and related structures of mathematical and physical sciences.
Journal of Homotopy and Related Structures is intended to publish papers on
Homotopy in the broad sense and its related areas like Homological and homotopical algebra, K-theory, topology of manifolds, geometric and categorical structures, homology theories, topological groups and algebras, stable homotopy theory, group actions, algebraic varieties, category theory, cobordism theory, controlled topology, noncommutative geometry, motivic cohomology, differential topology, algebraic geometry.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


