Geometric characterization of the persistence of 1D maps.

Abstract

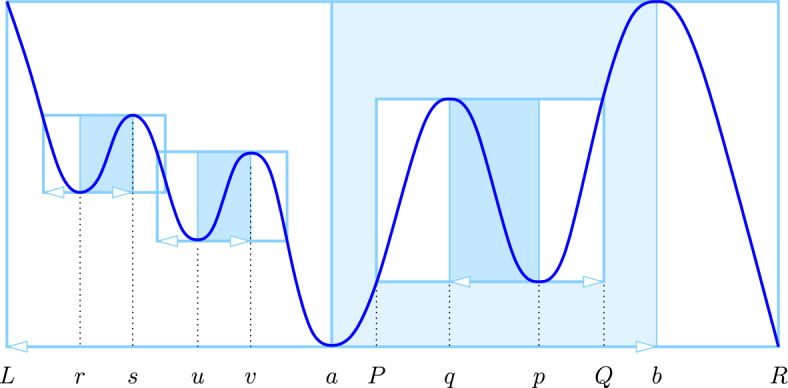
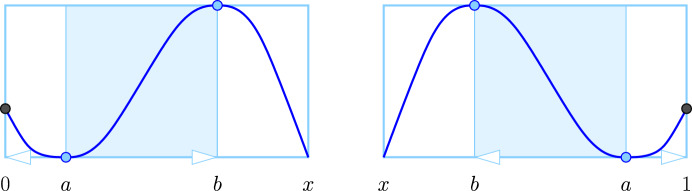
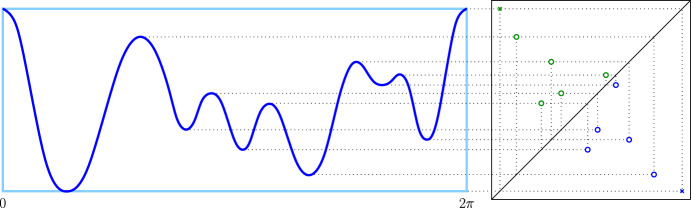
We characterize critical points of 1-dimensional maps paired in persistent homology geometrically and this way get elementary proofs of theorems about the symmetry of persistence diagrams and the variation of such maps. In particular, we identify branching points and endpoints of networks as the sole source of asymmetry and relate the cycle basis in persistent homology with a version of the stable marriage problem. Our analysis provides the foundations of fast algorithms for maintaining a collection of sorted lists together with its persistence diagram.