Homotopical perspective on statistical quantities
IF 0.5
4区 数学
引用次数: 0
Abstract
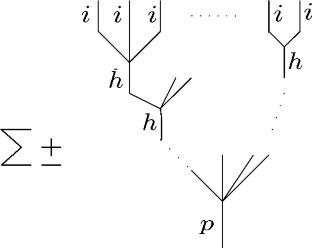
We introduce the notion of cumulants as applied to linear maps between associative (or commutative) algebras that are not compatible with the algebraic product structure. These cumulants have a close relationship with \(A_{\infty }\) and \(C_{\infty }\) morphisms, which are the classical homotopical tools for analyzing deformations of algebraically compatible linear maps. We look at these two different perspectives to understand how infinity-morphisms might inform our understanding of cumulants. We show that in the presence of an \(A_{\infty }\) or \(C_{\infty }\) morphism, the relevant cumulants are strongly homotopic to zero.
统计量的同调透视
我们将累积量的概念应用于与代数积结构不相容的结合代数(或交换代数)之间的线性映射。这些累积量与\(A_{\infty }\)和\(C_{\infty }\)态射密切相关,它们是分析代数相容线性映射变形的经典同调工具。我们从这两种不同的角度来理解无穷态是如何影响我们对累积量的理解的。我们证明了在\(A_{\infty }\)或\(C_{\infty }\)态射存在的情况下,相关的累积量是强同伦于零的。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Homotopy and Related Structures
Mathematics-Geometry and Topology
自引率
0.00%
发文量
0
期刊介绍:
Journal of Homotopy and Related Structures (JHRS) is a fully refereed international journal dealing with homotopy and related structures of mathematical and physical sciences.
Journal of Homotopy and Related Structures is intended to publish papers on
Homotopy in the broad sense and its related areas like Homological and homotopical algebra, K-theory, topology of manifolds, geometric and categorical structures, homology theories, topological groups and algebras, stable homotopy theory, group actions, algebraic varieties, category theory, cobordism theory, controlled topology, noncommutative geometry, motivic cohomology, differential topology, algebraic geometry.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


