Twisting structures and morphisms up to strong homotopy
IF 0.7
4区 数学
Q2 MATHEMATICS
引用次数: 0
Abstract
We define twisted composition products of symmetric sequences via classifying morphisms rather than twisting cochains. Our approach allows us to establish an adjunction that simultaneously generalizes a classic one for algebras and coalgebras, and the bar-cobar adjunction for quadratic operads. The comonad associated to this adjunction turns out to be, in several cases, a standard Koszul construction. The associated Kleisli categories are the “strong homotopy” morphism categories. In an appendix, we study the co-ring associated to the canonical morphism of cooperads , which is exactly the two-sided Koszul resolution of the associative operad
, also known as the Alexander-Whitney co-ring.
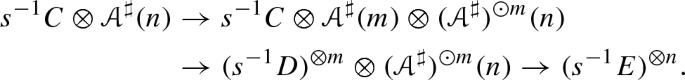
到强同伦的扭曲结构和态射
本文通过对对称序列的态射分类来定义对称序列的扭曲复合积,而不是通过对扭曲协链的分类来定义对称序列的扭曲复合积。我们的方法允许我们建立一个同时推广经典代数和余代数的附加,以及二次操作数的条形-条形附加。在一些情况下,与这个连词相关的共同语是一个标准的Koszul结构。相关的Kleisli范畴是“强同伦”态射范畴。在附录中,我们研究了与合作算子正则态射相关的共环,它正是结合算子的双面Koszul解析,也称为Alexander-Whitney共环。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Homotopy and Related Structures
MATHEMATICS-
CiteScore
1.20
自引率
0.00%
发文量
21
审稿时长
>12 weeks
期刊介绍:
Journal of Homotopy and Related Structures (JHRS) is a fully refereed international journal dealing with homotopy and related structures of mathematical and physical sciences.
Journal of Homotopy and Related Structures is intended to publish papers on
Homotopy in the broad sense and its related areas like Homological and homotopical algebra, K-theory, topology of manifolds, geometric and categorical structures, homology theories, topological groups and algebras, stable homotopy theory, group actions, algebraic varieties, category theory, cobordism theory, controlled topology, noncommutative geometry, motivic cohomology, differential topology, algebraic geometry.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


