The Elastic Properties of Dilute Solid Suspensions with Imperfect Interfacial Bonding: Variational Approximations Versus Full-Field Simulations

Abstract

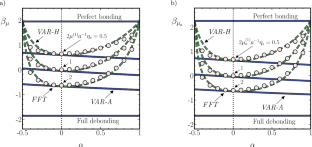
Approximations for the elastic properties of dilute solid suspensions with imperfect interfacial bonding are derived and assessed. A variational procedure is employed in such a way that the resulting approximations reproduce exact results for weakly anisotropic but otherwise arbitrarily large interfacial compliances. Two approximations are generated which display the exact same format but differ in the way the interfacial compliance is averaged over the interfaces: the first approximation depends on an ‘arithmetic’ mean while the second approximation depends on a ‘harmonic’ mean. Both approximations allow for arbitrary elastic anisotropy of the constitutive phases but are restricted to suspended inclusions of spherical shape. The approximations are applied to a class of isotropic suspensions and confronted to full-field numerical simulations for assessment. Simulations are performed by means of a Fast Fourier Transform algorithm suitably implemented to handle dilute suspensions with imperfect interfaces. Also included in the comparisons are available results for suspensions with extremely anisotropic bondings. Overall, the ‘harmonic’ approximation is found to be much more precise than the ‘arithmetic’ approximation. The finding is of practical relevance given the widespread use of ‘arithmetic’ approximations in existing descriptions based on modified Eshelby tensors.