Density Function of Weighted Sum of Chi-Square Variables with Trigonometric Weights

IF 1 Q4 OPTICS

Optical Memory and Neural Networks Pub Date : 2023-04-02 DOI:10.3103/S1060992X23010071

V. I. Egorov, B. V. Kryzhanovsky

引用次数: 0

Abstract

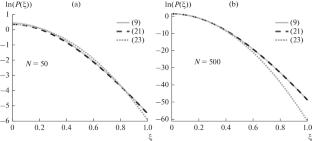
We have investigated a weighted chi-square distribution of the variable ξ which is a weighted sum of squared normally distributed independent variables whose weights are cosines of angles \({{\varphi }_{k}} = {{2\pi k} \mathord{\left/ {\vphantom {{2\pi k} N}} \right. \kern-0em} N},\) where \(k \in \left\{ {0,1,...,N - 1} \right\}\) and N is the number of the freedom degrees. We have found the exact expression for the density function of this distribution and its approximation for large N. The distribution is compared with the Gaussian distribution.

Abstract Image

查看原文本刊更多论文

三角加权卡方变量和的密度函数

我们研究了变量ξ的加权卡方分布，它是正态分布自变量的加权平方和，其权重为角度的余弦\({{\varphi }_{k}} = {{2\pi k} \mathord{\left/ {\vphantom {{2\pi k} N}} \right. \kern-0em} N},\)，其中\(k \in \left\{ {0,1,...,N - 1} \right\}\)和N是自由度的数量。我们已经找到了这个分布的密度函数的精确表达式以及它在大n时的近似。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Optical Memory and Neural Networks OPTICS-

CiteScore

1.50

自引率

11.10%

发文量

期刊介绍： The journal covers a wide range of issues in information optics such as optical memory, mechanisms for optical data recording and processing, photosensitive materials, optical, optoelectronic and holographic nanostructures, and many other related topics. Papers on memory systems using holographic and biological structures and concepts of brain operation are also included. The journal pays particular attention to research in the field of neural net systems that may lead to a new generation of computional technologies by endowing them with intelligence.