Error Bounds for Dynamical Spectral Estimation.
IF 2.6
Q1 MATHEMATICS, APPLIED
SIAM journal on mathematics of data science
Pub Date : 2021-01-01
Epub Date: 2021-02-11
DOI:10.1137/20m1335984
引用次数: 0
Abstract
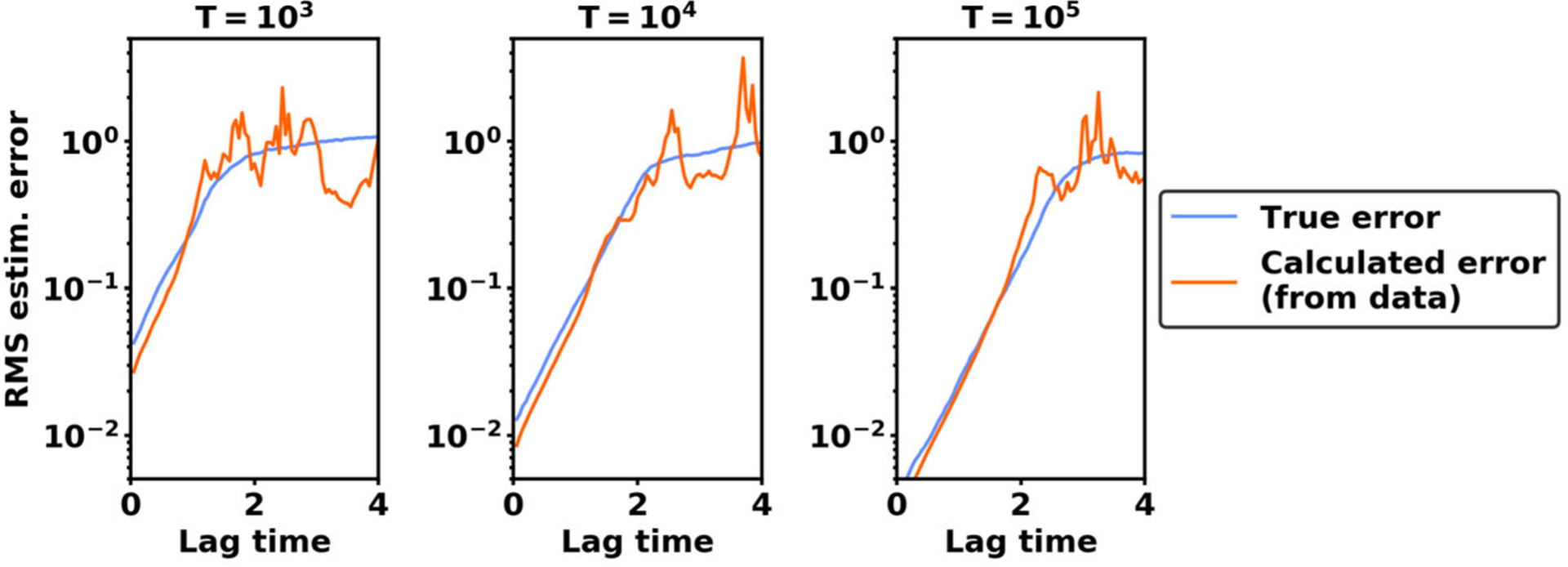
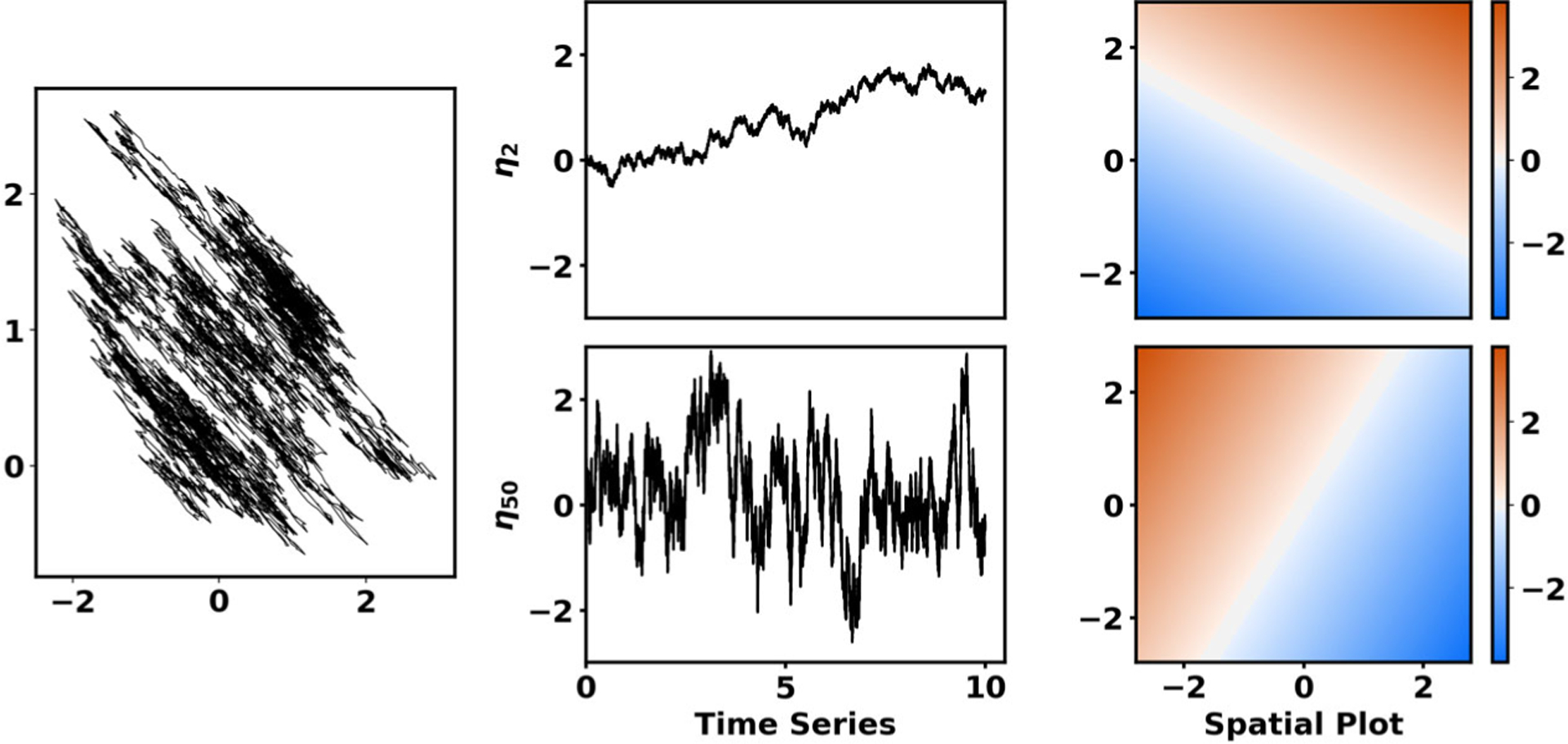
Dynamical spectral estimation is a well-established numerical approach for estimating eigenvalues and eigenfunctions of the Markov transition operator from trajectory data. Although the approach has been widely applied in biomolecular simulations, its error properties remain poorly understood. Here we analyze the error of a dynamical spectral estimation method called "the variational approach to conformational dynamics" (VAC). We bound the approximation error and estimation error for VAC estimates. Our analysis establishes VAC's convergence properties and suggests new strategies for tuning VAC to improve accuracy.

动态频谱估算的误差限。
动态谱估计是从轨迹数据中估算马尔可夫转换算子特征值和特征函数的一种成熟的数值方法。虽然这种方法已广泛应用于生物分子模拟,但人们对其误差特性仍然知之甚少。在此,我们分析了一种名为 "构象动力学变分法"(VAC)的动态谱估计方法的误差。我们对 VAC 估计的近似误差和估计误差进行了约束。我们的分析确定了 VAC 的收敛特性,并提出了调整 VAC 以提高准确性的新策略。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


