The existence of nonnegative solutions for a nonlinear fractional q-differential problem via a different numerical approach.

IF 1.6 3区数学 Q1 Mathematics

Journal of Inequalities and Applications Pub Date : 2021-01-01 Epub Date: 2021-04-23 DOI:10.1186/s13660-021-02612-z

Mohammad Esmael Samei, Ahmad Ahmadi, Sayyedeh Narges Hajiseyedazizi, Shashi Kant Mishra, Bhagwat Ram

{"title":"The existence of nonnegative solutions for a nonlinear fractional q-differential problem via a different numerical approach.","authors":"Mohammad Esmael Samei, Ahmad Ahmadi, Sayyedeh Narges Hajiseyedazizi, Shashi Kant Mishra, Bhagwat Ram","doi":"10.1186/s13660-021-02612-z","DOIUrl":null,"url":null,"abstract":"This paper deals with the existence of nonnegative solutions for a class of boundary value problems of fractional q-differential equation <math><mmultiscripts><mi>D</mi> <mi>q</mi> <mi>σ</mi> <mprescripts></mprescripts> <none></none> <mi>c</mi></mmultiscripts> <mo>[</mo> <mi>k</mi> <mo>]</mo> <mo>(</mo> <mi>t</mi> <mo>)</mo> <mo>=</mo> <mi>w</mi> <mo>(</mo> <mi>t</mi> <mo>,</mo> <mi>k</mi> <mo>(</mo> <mi>t</mi> <mo>)</mo> <mo>,</mo> <msup><mrow></mrow> <mi>c</mi></msup> <msubsup><mi>D</mi> <mi>q</mi> <mi>ζ</mi></msubsup> <mo>[</mo> <mi>k</mi> <mo>]</mo> <mo>(</mo> <mi>t</mi> <mo>)</mo> <mo>)</mo></math> with three-point conditions for <math><mi>t</mi> <mo>∈</mo> <mo>(</mo> <mn>0</mn> <mo>,</mo> <mn>1</mn> <mo>)</mo></math> on a time scale <math><msub><mi>T</mi> <msub><mi>t</mi> <mn>0</mn></msub> </msub> <mo>=</mo> <mo>{</mo> <mi>t</mi> <mo>:</mo> <mi>t</mi> <mo>=</mo> <msub><mi>t</mi> <mn>0</mn></msub> <msup><mi>q</mi> <mi>n</mi></msup> <mo>}</mo> <mo>∪</mo> <mo>{</mo> <mn>0</mn> <mo>}</mo></math> , where <math><mi>n</mi> <mo>∈</mo> <mi>N</mi></math> , <math><msub><mi>t</mi> <mn>0</mn></msub> <mo>∈</mo> <mi>R</mi></math> , and <math><mn>0</mn> <mo><</mo> <mi>q</mi> <mo><</mo> <mn>1</mn></math> , based on the Leray-Schauder nonlinear alternative and Guo-Krasnoselskii theorem. Moreover, we discuss the existence of nonnegative solutions. Examples involving algorithms and illustrated graphs are presented to demonstrate the validity of our theoretical findings.","PeriodicalId":49163,"journal":{"name":"Journal of Inequalities and Applications","volume":null,"pages":null},"PeriodicalIF":1.6000,"publicationDate":"2021-01-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://sci-hub-pdf.com/10.1186/s13660-021-02612-z","citationCount":"8","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Inequalities and Applications","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1186/s13660-021-02612-z","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"2021/4/23 0:00:00","PubModel":"Epub","JCR":"Q1","JCRName":"Mathematics","Score":null,"Total":0}

引用次数: 8

Abstract

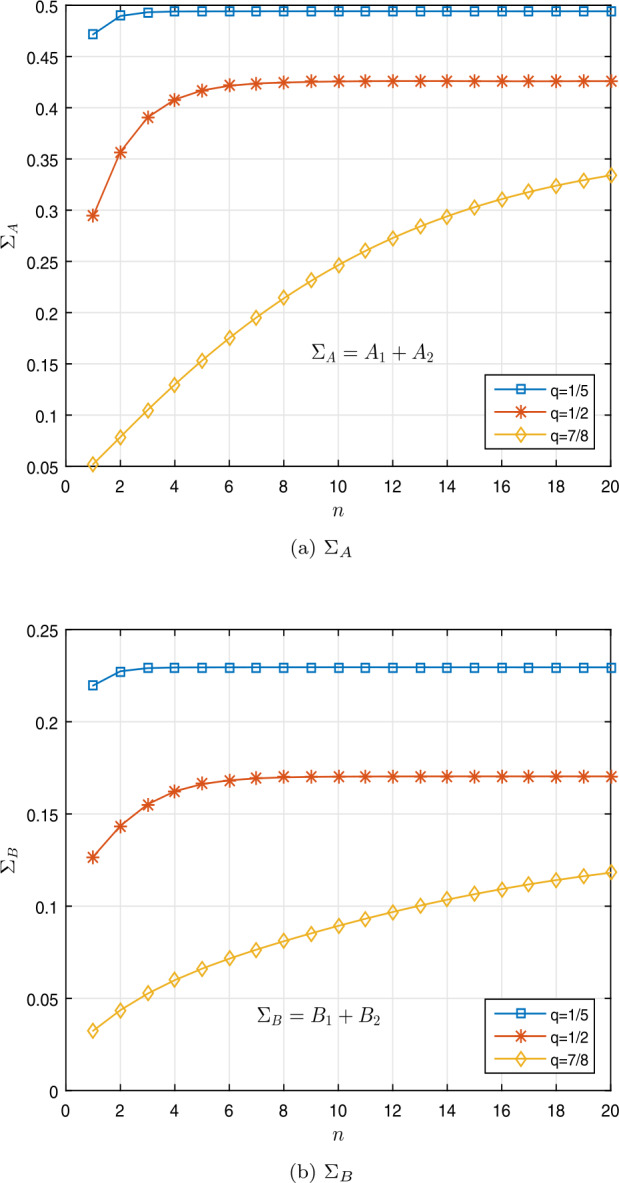
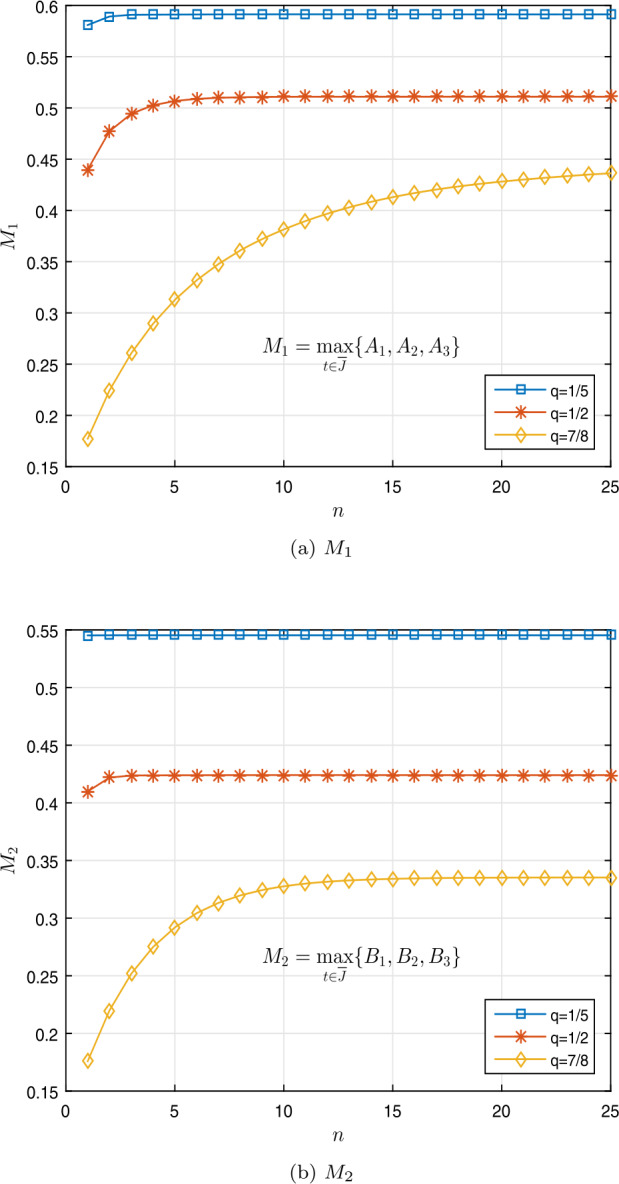
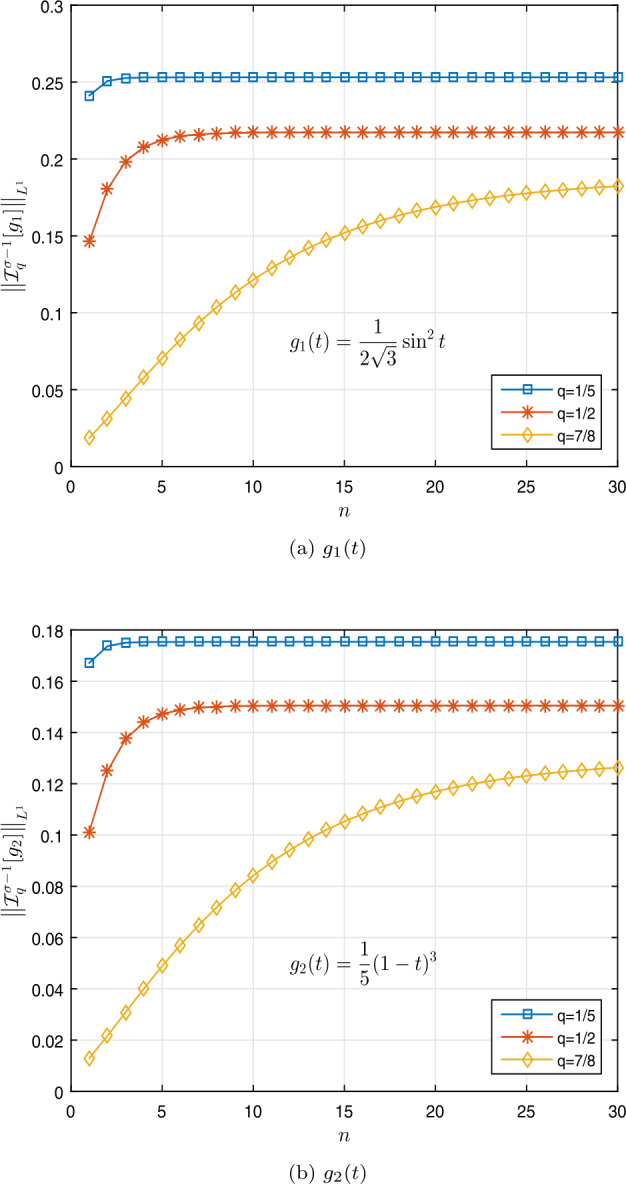
This paper deals with the existence of nonnegative solutions for a class of boundary value problems of fractional q-differential equation ${}^{c}D_{q}^{σ} [k] (t) = w (t, k (t),^{c} D_{q}^{ζ} [k] (t))$ with three-point conditions for $t \in (0, 1)$ on a time scale $T_{t_{0}} = {t : t = t_{0} q^{n}} \cup {0}$ , where $n \in N$ , $t_{0} \in R$ , and $0 < q < 1$ , based on the Leray-Schauder nonlinear alternative and Guo-Krasnoselskii theorem. Moreover, we discuss the existence of nonnegative solutions. Examples involving algorithms and illustrated graphs are presented to demonstrate the validity of our theoretical findings.

Abstract Image

查看原文本刊更多论文

用不同的数值方法研究非线性分数阶q微分问题非负解的存在性。

摘要非负解的存在性的一类边值问题部分q-differential方程D qσc [k] (t) = w (t, k (t), c D qζ[k] (t))三点条件t∈(0,1)时间尺度t t 0 = {q t: t = 0 n}∪{0},其中n∈n t 0∈R, q和0 1,基于Leray-Schauder非线性替代和Guo-Krasnoselskii定理。此外，我们还讨论了非负解的存在性。举例涉及算法和图解的图表，以证明我们的理论发现的有效性。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Journal of Inequalities and Applications MATHEMATICS, APPLIED-MATHEMATICS

CiteScore

3.30

自引率

6.20%

发文量

136

审稿时长

3 months

期刊介绍： The aim of this journal is to provide a multi-disciplinary forum of discussion in mathematics and its applications in which the essentiality of inequalities is highlighted. This Journal accepts high quality articles containing original research results and survey articles of exceptional merit. Subject matters should be strongly related to inequalities, such as, but not restricted to, the following: inequalities in analysis, inequalities in approximation theory, inequalities in combinatorics, inequalities in economics, inequalities in geometry, inequalities in mechanics, inequalities in optimization, inequalities in stochastic analysis and applications.