A fractional complex network model for novel corona virus in China.

IF 4.1 3区数学 Q1 Mathematics

Advances in Difference Equations Pub Date : 2021-01-01 Epub Date: 2021-01-06 DOI:10.1186/s13662-020-03182-y

H A A El-Saka, I Obaya, H N Agiza

引用次数: 4

Abstract

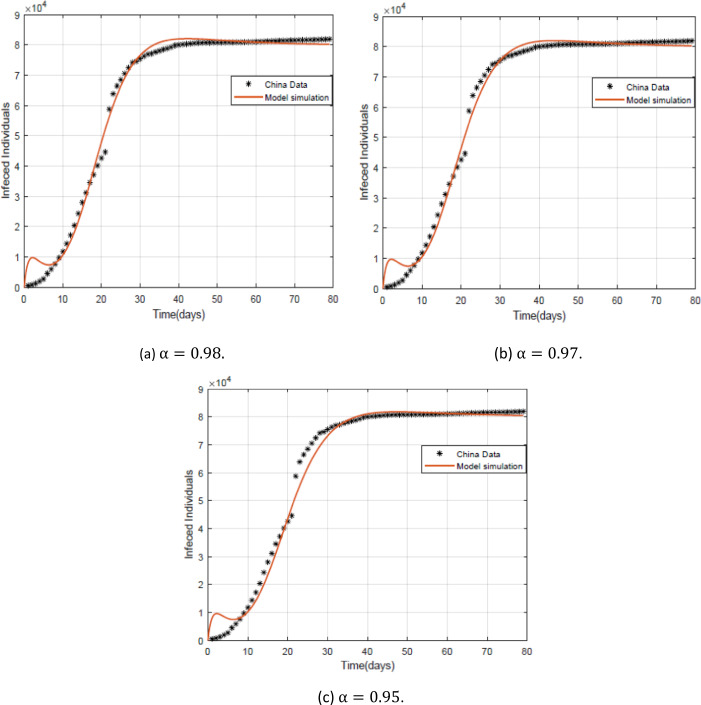
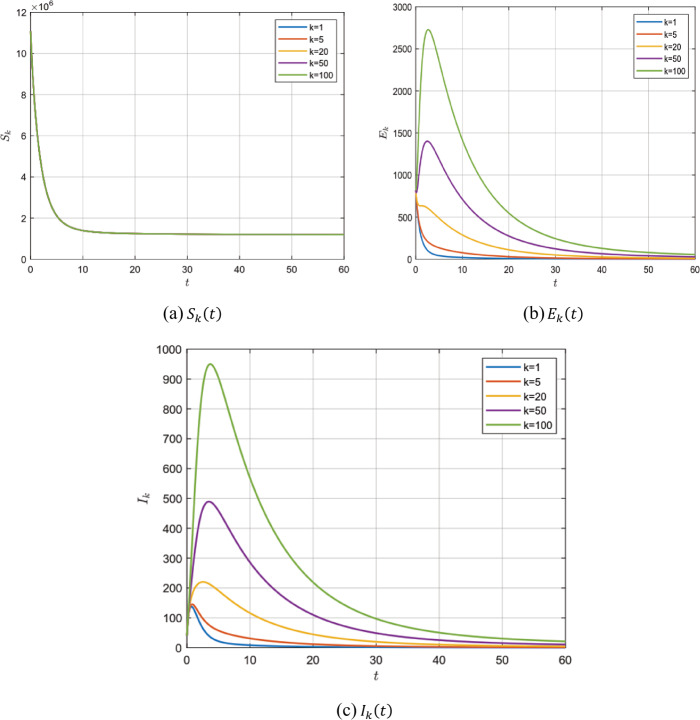
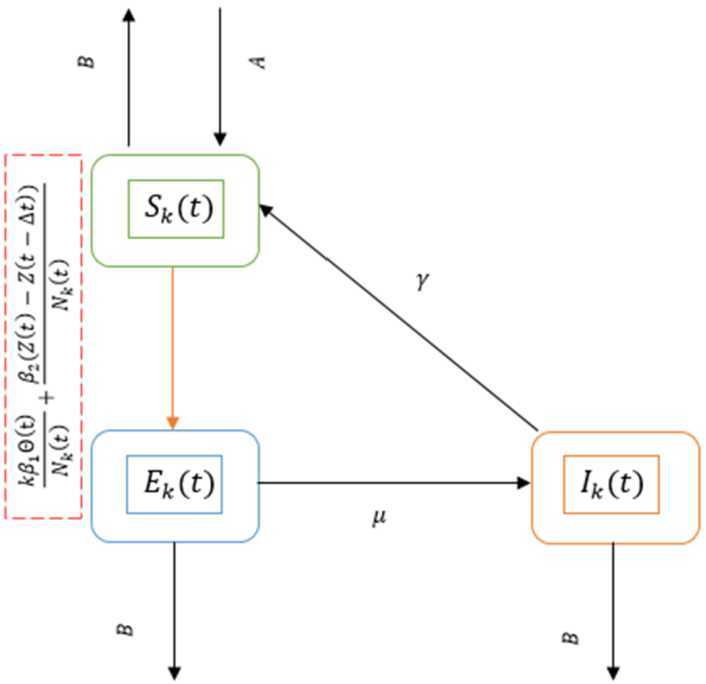
As is well known the novel coronavirus (COVID-19) is a zoonotic virus and our model is concerned with the effect of the zoonotic source of the coronavirus during the outbreak in China. We present a SEIS complex network epidemic model for the novel coronavirus. Our model is presented in fractional form and with varying population. The steady states and the basic reproductive number are calculated. We also present some numerical examples and the sensitivity analysis of the basic reproductive number for the parameters.

Abstract Image

查看原文本刊更多论文

中国新型冠状病毒分式复杂网络模型

众所周知，新型冠状病毒(COVID-19)是一种人畜共患病毒，我们的模型关注的是在中国疫情期间冠状病毒人畜共患源的影响。提出了一种新型冠状病毒的SEIS复杂网络流行病模型。我们的模型以分数形式呈现，并具有不同的人口。计算了稳态和基本再生数。给出了一些数值算例，并对参数的基本再生数进行了灵敏度分析。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Advances in Difference Equations 数学-数学

自引率

0.00%

发文量

审稿时长

4-8 weeks

期刊介绍： The theory of difference equations, the methods used, and their wide applications have advanced beyond their adolescent stage to occupy a central position in applicable analysis. In fact, in the last 15 years, the proliferation of the subject has been witnessed by hundreds of research articles, several monographs, many international conferences, and numerous special sessions. The theory of differential and difference equations forms two extreme representations of real world problems. For example, a simple population model when represented as a differential equation shows the good behavior of solutions whereas the corresponding discrete analogue shows the chaotic behavior. The actual behavior of the population is somewhere in between. The aim of Advances in Difference Equations is to report mainly the new developments in the field of difference equations, and their applications in all fields. We will also consider research articles emphasizing the qualitative behavior of solutions of ordinary, partial, delay, fractional, abstract, stochastic, fuzzy, and set-valued differential equations. Advances in Difference Equations will accept high-quality articles containing original research results and survey articles of exceptional merit.