Optimal minimum variance-entropy control of tumour growth processes based on the Fokker–Planck equation
Abstract
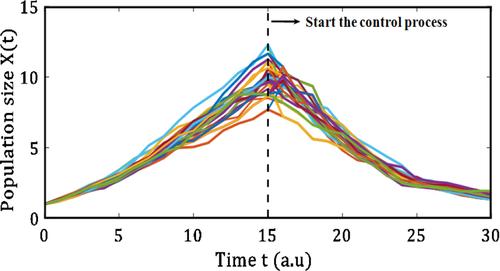
The authors demonstrated an optimal stochastic control algorithm to obtain desirable cancer treatment based on the Gompertz model. Two external forces as two time-dependent functions are presented to manipulate the growth and death rates in the drift term of the Gompertz model. These input signals represent the effect of external treatment agents to decrease tumour growth rate and increase tumour death rate, respectively. Entropy and variance of cancerous cells are simultaneously controlled based on the Gompertz model. They have introduced a constrained optimisation problem whose cost function is the variance of a cancerous cells population. The defined entropy is based on the probability density function of affected cells was used as a constraint for the cost function. Analysing growth and death rates of cancerous cells, it is found that the logarithmic control signal reduces the growth rate, while the hyperbolic tangent–like control function increases the death rate of tumour growth. The two optimal control signals were calculated by converting the constrained optimisation problem into an unconstrained optimisation problem and by using the real–coded genetic algorithm. Mathematical justifications are implemented to elucidate the existence and uniqueness of the solution for the optimal control problem.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


