Global dynamics of a novel deterministic and stochastic SIR epidemic model with vertical transmission and media coverage.

IF 4.1 3区数学 Q1 Mathematics

Advances in Difference Equations Pub Date : 2020-01-01 Epub Date: 2020-12-04 DOI:10.1186/s13662-020-03145-3

Xiaodong Wang, Chunxia Wang, Kai Wang

引用次数: 3

Abstract

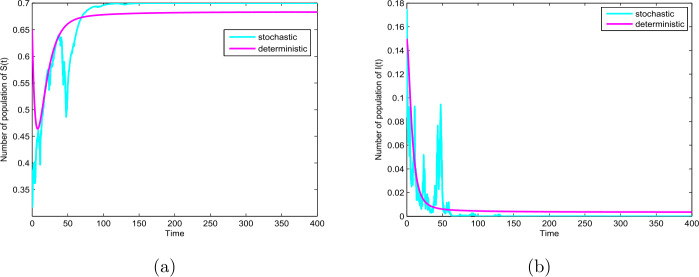
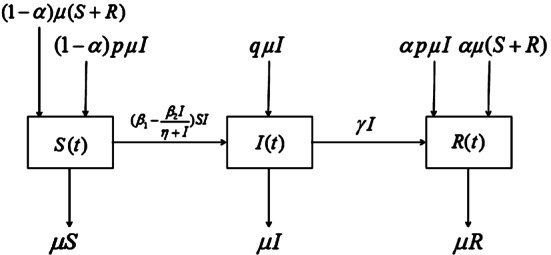
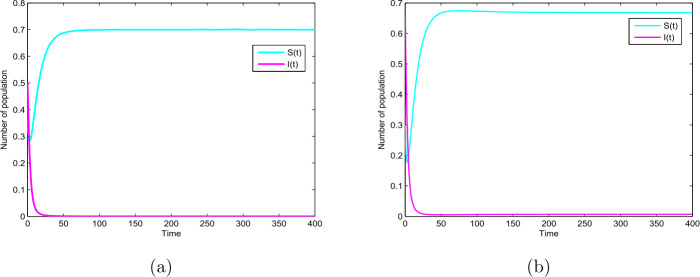
In this paper, we study a novel deterministic and stochastic SIR epidemic model with vertical transmission and media coverage. For the deterministic model, we give the basic reproduction number $R_{0}$ which determines the extinction or prevalence of the disease. In addition, for the stochastic model, we prove existence and uniqueness of the positive solution, and extinction and persistence in mean. Furthermore, we give numerical simulations to verify our results.

Abstract Image

查看原文本刊更多论文

具有垂直传播和媒体覆盖的新型确定性和随机SIR流行病模型的全球动力学。

本文研究了一种具有垂直传播和媒介覆盖的确定性随机SIR流行病模型。对于确定性模型，我们给出了决定疾病灭绝或流行的基本繁殖数r0。此外，对于随机模型，我们证明了正解的存在唯一性，以及均值的消去和持续性。最后给出了数值模拟结果。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Advances in Difference Equations 数学-数学

自引率

0.00%

发文量

审稿时长

4-8 weeks

期刊介绍： The theory of difference equations, the methods used, and their wide applications have advanced beyond their adolescent stage to occupy a central position in applicable analysis. In fact, in the last 15 years, the proliferation of the subject has been witnessed by hundreds of research articles, several monographs, many international conferences, and numerous special sessions. The theory of differential and difference equations forms two extreme representations of real world problems. For example, a simple population model when represented as a differential equation shows the good behavior of solutions whereas the corresponding discrete analogue shows the chaotic behavior. The actual behavior of the population is somewhere in between. The aim of Advances in Difference Equations is to report mainly the new developments in the field of difference equations, and their applications in all fields. We will also consider research articles emphasizing the qualitative behavior of solutions of ordinary, partial, delay, fractional, abstract, stochastic, fuzzy, and set-valued differential equations. Advances in Difference Equations will accept high-quality articles containing original research results and survey articles of exceptional merit.