Existence theory and numerical analysis of three species prey-predator model under Mittag-Leffler power law.

IF 4.1 3区数学 Q1 Mathematics

Advances in Difference Equations Pub Date : 2020-01-01 Epub Date: 2020-05-27 DOI:10.1186/s13662-020-02709-7

Mohammed S Abdo, Satish K Panchal, Kamal Shah, Thabet Abdeljawad

引用次数: 28

Abstract

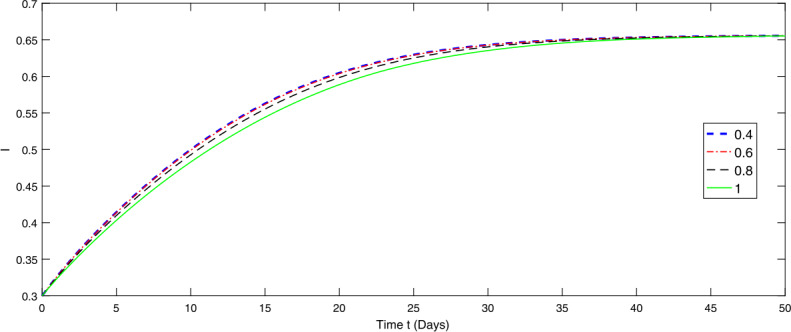
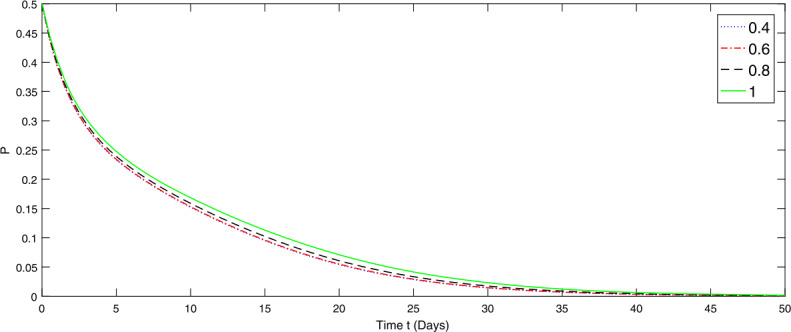
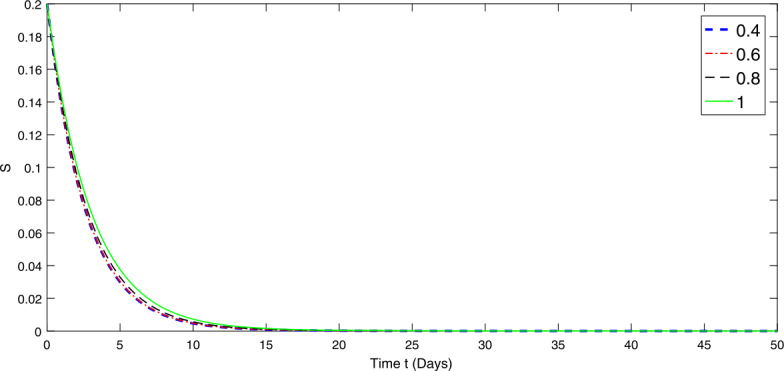
In this manuscript, the fractional Atangana-Baleanu-Caputo model of prey and predator is studied theoretically and numerically. The existence and Ulam-Hyers stability results are obtained by applying fixed point theory and nonlinear analysis. The approximation solutions for the considered model are discussed via the fractional Adams Bashforth method. Moreover, the behavior of the solution to the given model is explained by graphical representations through the numerical simulations. The obtained results play an important role in developing the theory of fractional analytical dynamic of many biological systems.

Abstract Image

查看原文本刊更多论文

Mittag-Leffler幂律下三物种捕食-捕食模型的存在性理论及数值分析。

本文从理论上和数值上研究了捕食者和猎物的分数Atangana-Baleanu-Caputo模型。应用不动点理论和非线性分析，得到了系统的存在性和Ulam-Hyers稳定性结果。通过分数阶Adams Bashforth方法讨论了所考虑模型的近似解。此外，通过数值模拟，用图形表示解释了给定模型解的行为。所得结果对许多生物系统的分数分析动力学理论的发展具有重要作用。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Advances in Difference Equations 数学-数学

自引率

0.00%

发文量

审稿时长

4-8 weeks

期刊介绍： The theory of difference equations, the methods used, and their wide applications have advanced beyond their adolescent stage to occupy a central position in applicable analysis. In fact, in the last 15 years, the proliferation of the subject has been witnessed by hundreds of research articles, several monographs, many international conferences, and numerous special sessions. The theory of differential and difference equations forms two extreme representations of real world problems. For example, a simple population model when represented as a differential equation shows the good behavior of solutions whereas the corresponding discrete analogue shows the chaotic behavior. The actual behavior of the population is somewhere in between. The aim of Advances in Difference Equations is to report mainly the new developments in the field of difference equations, and their applications in all fields. We will also consider research articles emphasizing the qualitative behavior of solutions of ordinary, partial, delay, fractional, abstract, stochastic, fuzzy, and set-valued differential equations. Advances in Difference Equations will accept high-quality articles containing original research results and survey articles of exceptional merit.