Quadrics and Scherk towers.
IF 0.8
4区 数学
Q2 MATHEMATICS
Monatshefte fur Mathematik
Pub Date : 2018-01-01
Epub Date: 2017-07-03
DOI:10.1007/s00605-017-1075-5
引用次数: 3
Abstract
We investigate the relation between quadrics and their Christoffel duals on the one hand, and certain zero mean curvature surfaces and their Gauss maps on the other hand. To study the relation between timelike minimal surfaces and the Christoffel duals of 1-sheeted hyperboloids we introduce para-holomorphic elliptic functions. The curves of type change for real isothermic surfaces of mixed causal type turn out to be aligned with the real curvature line net.
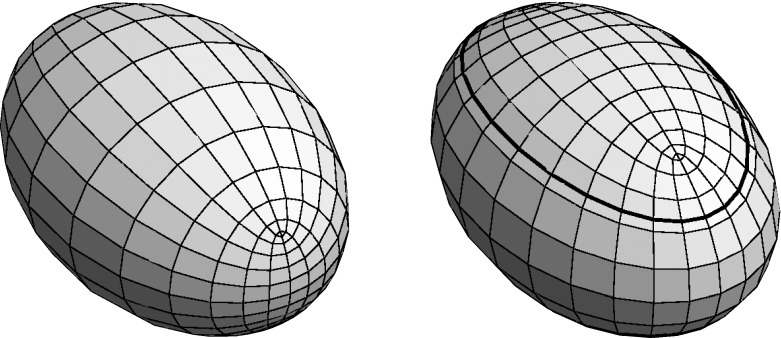

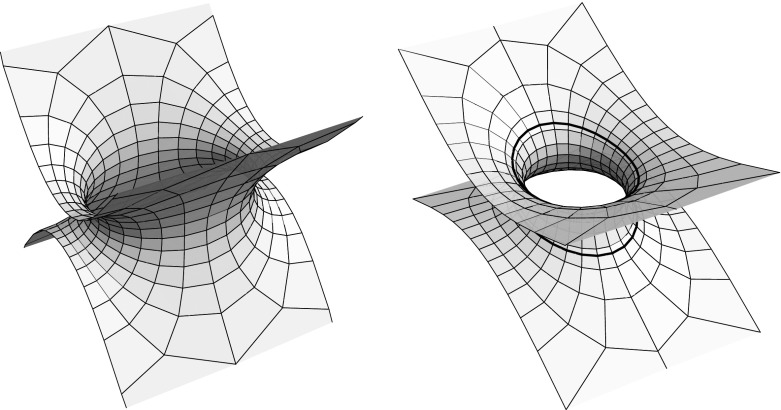
二次曲线和舍尔克塔。
我们一方面研究了二次曲面和它们的克里斯托费尔对偶之间的关系,另一方面研究了某些零平均曲率曲面和它们的高斯映射之间的关系。为了研究类时极小曲面与1片双曲面的克里斯托费尔对偶之间的关系,引入了准全纯椭圆函数。混合因果型实际等温线面的类型变化曲线与实际曲率线网一致。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.60
自引率
11.10%
发文量
155
审稿时长
4-8 weeks
期刊介绍:
The journal was founded in 1890 by G. v. Escherich and E. Weyr as "Monatshefte für Mathematik und Physik" and appeared with this title until 1944. Continued from 1948 on as "Monatshefte für Mathematik", its managing editors were L. Gegenbauer, F. Mertens, W. Wirtinger, H. Hahn, Ph. Furtwängler, J. Radon, K. Mayrhofer, N. Hofreiter, H. Reiter, K. Sigmund, J. Cigler.
The journal is devoted to research in mathematics in its broadest sense. Over the years, it has attracted a remarkable cast of authors, ranging from G. Peano, and A. Tauber to P. Erdös and B. L. van der Waerden. The volumes of the Monatshefte contain historical achievements in analysis (L. Bieberbach, H. Hahn, E. Helly, R. Nevanlinna, J. Radon, F. Riesz, W. Wirtinger), topology (K. Menger, K. Kuratowski, L. Vietoris, K. Reidemeister), and number theory (F. Mertens, Ph. Furtwängler, E. Hlawka, E. Landau). It also published landmark contributions by physicists such as M. Planck and W. Heisenberg and by philosophers such as R. Carnap and F. Waismann. In particular, the journal played a seminal role in analyzing the foundations of mathematics (L. E. J. Brouwer, A. Tarski and K. Gödel).
The journal publishes research papers of general interest in all areas of mathematics. Surveys of significant developments in the fields of pure and applied mathematics and mathematical physics may be occasionally included.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


