Maximum norm error estimates of fourth-order compact difference scheme for the nonlinear Schrödinger equation involving a quintic term.

IF 1.6 3区数学 Q1 Mathematics

Journal of Inequalities and Applications Pub Date : 2018-01-01 Epub Date: 2018-07-20 DOI:10.1186/s13660-018-1775-y

Hanqing Hu, Hanzhang Hu

引用次数: 3

Abstract

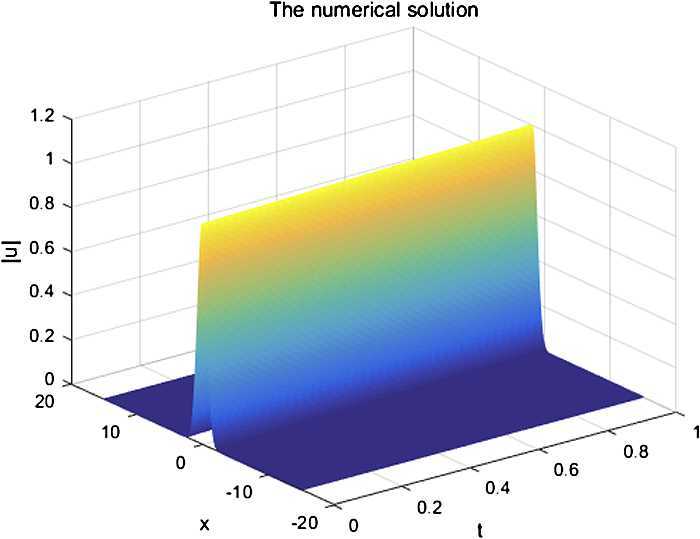
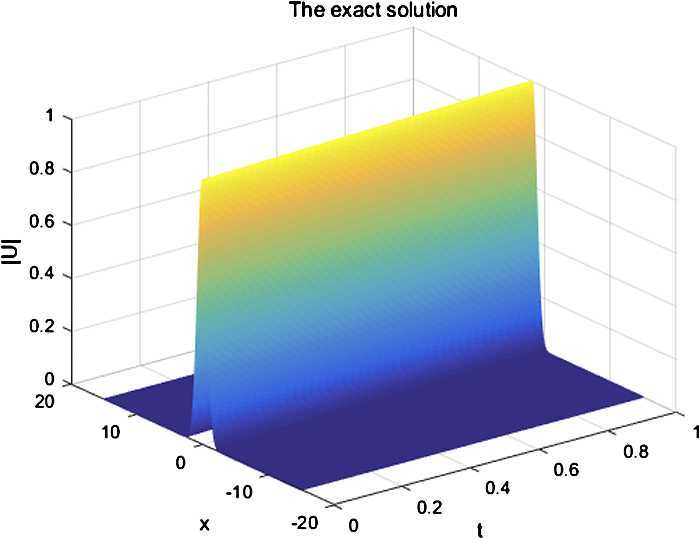
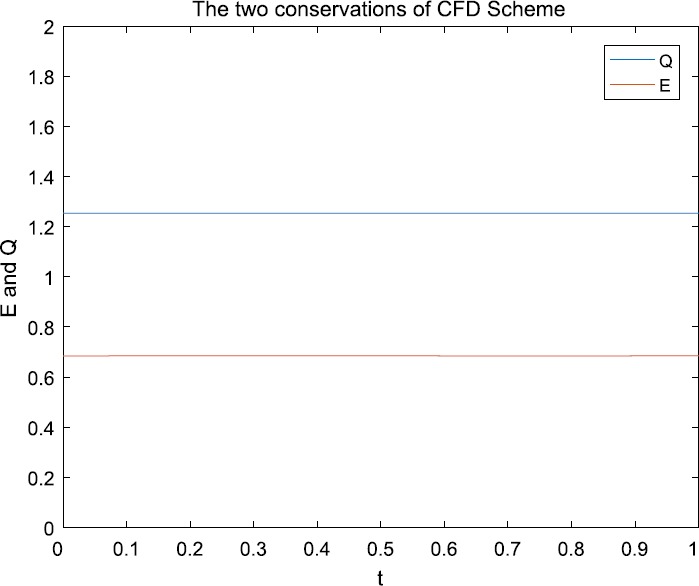
A compact finite difference (CFD) scheme is presented for the nonlinear Schrödinger equation involving a quintic term. The two discrete conservative laws are obtained. The unconditional stability and convergence in maximum norm with order $O (τ^{2} + h^{4})$ are proved by using the energy method. A numerical experiment is presented to support our theoretical results.

Abstract Image

查看原文本刊更多论文

含五次项的非线性Schrödinger方程的四阶紧致差分格式的最大范数误差估计。

针对含有五次项的非线性Schrödinger方程，提出了一种紧凑的有限差分格式。得到了两个离散的守恒律。利用能量法证明了该方法在O(τ2+h4)阶最大范数下的无条件稳定性和收敛性。通过数值实验验证了理论结果。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Journal of Inequalities and Applications MATHEMATICS, APPLIED-MATHEMATICS

CiteScore

3.30

自引率

6.20%

发文量

136

审稿时长

3 months

期刊介绍： The aim of this journal is to provide a multi-disciplinary forum of discussion in mathematics and its applications in which the essentiality of inequalities is highlighted. This Journal accepts high quality articles containing original research results and survey articles of exceptional merit. Subject matters should be strongly related to inequalities, such as, but not restricted to, the following: inequalities in analysis, inequalities in approximation theory, inequalities in combinatorics, inequalities in economics, inequalities in geometry, inequalities in mechanics, inequalities in optimization, inequalities in stochastic analysis and applications.