Equivariant Oka theory: survey of recent progress.
Complex analysis and its synergies
Pub Date : 2022-01-01
Epub Date: 2022-08-24
DOI:10.1007/s40627-022-00103-5
引用次数: 2
Abstract
We survey recent work, published since 2015, on equivariant Oka theory. The main results described in the survey are as follows. Homotopy principles for equivariant isomorphisms of Stein manifolds on which a reductive complex Lie group G acts. Applications to the linearisation problem. A parametric Oka principle for sections of a bundle E of homogeneous spaces for a group bundle , all over a reduced Stein space X with compatible actions of a reductive complex group on E, , and X. Application to the classification of generalised principal bundles with a group action. Finally, an equivariant version of Gromov's Oka principle based on a notion of a G-manifold being G-Oka.
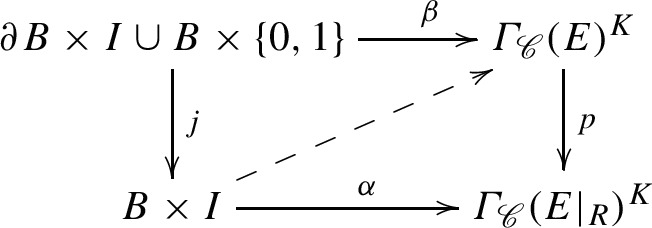
等变Oka理论:最新进展综述。
我们调查了自2015年以来发表的关于等变Oka理论的最新研究。调查中描述的主要结果如下。复李群G作用于Stein流形的等变同构的同伦原理。线性化问题的应用。关于群束G在约化Stein空间X上具有约化复群在E、G、X上的相容作用的齐次空间束E的截面的参数Oka原理。最后,基于g流形为G-Oka的概念,给出了Gromov的Oka原理的等变版本。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


