Quantum entropy structural encoding for graph neural networks

Abstract

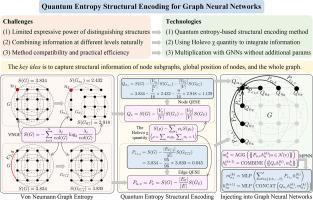
Structural encoding (SE) can improve the expressive power of Graph Neural Networks (GNNs). However, current SE methods have limited expressive power because they have limitations in capturing (1) node subgraphs, (2) global position of nodes, and (3) global structure of the graph. To tackle this challenge, we propose a Quantum Entropy Structural Encoding (QESE) for GNNs. For limitations (1) and (3), we employ quantum entropy on node subgraphs and the whole graph to recognize highly similar structures. For limitation (2), we apply quantum entropy on complement parts of node subgraphs for locating node positions. Then, we obtain QESE by integrating quantum entropies of these three parts through the Holevo $\chi$ quantity. Notably, we prove that QESE always captures structural distinction in node subgraphs and the whole graph, and the Holevo $\chi$ quantity empowers QESE to represent global position of nodes. We theoretically show that QESE distinguishes strongly regular graphs that 3-WL fails to, and has the potential to be more powerful than $k$-WL ($k$>3). We adopt a plug-and-play approach to inject QESE with existing GNNs, and further design an approximated version to reduce computational complexity. Experimental results show that QESE uplifts the expressive power of GNNs beyond 3-WL and indeed captures node subgraphs. Furthermore, QESE improves the performance of various GNNs in graph learning tasks and also surpasses other SE methods.