A Fractional-Order Mathematical Model for Obesity Dynamics: Analysis Via Hermite Wavelets and Comparative Numerical Methods

Abstract

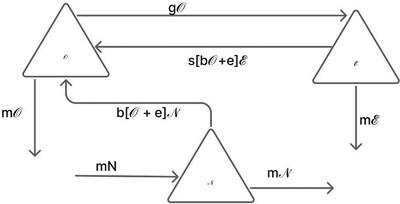
The dynamics of obesity are addressed in this study by formulating a fractional-order non-linear system that models the time-dependent behavior of three population groups: never obese, obese, and exobese people. Obesity has become one of the most significant global public health challenges, with its prevalence increasing steadily across all age groups due to factors such as lifestyle changes, urbanization, and dietary patterns. In this work, real-world data from Brunei Darussalam, covering the years 1990 to 2022, are incorporated to study obesity dynamics more realistically. In this article, the Hermite wavelet technique is employed as a numerical technique to solve the proposed system and analyze the time-dependent behavior of each group. To evaluate the accuracy of the Hermite wavelet method, its solutions are compared with the Runge-Kutta technique, a traditional fourth-order approach. The Adams-Bashforth-Moulton technique is compared with RK-4 to assess accuracy through absolute error analysis. Sensitivity analysis is also performed to investigate the influence of key model parameters on the system's behavior. Graphical and 3D visualizations illustrate the evolution of the population groups over time. Furthermore, a comprehensive theoretical framework is provided, including convergence, and verifying that the solution exists, is unique, and remains bounded.