Randomized methods for dynamical low-rank approximation

Abstract

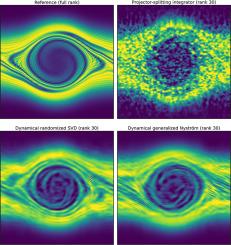
We introduce novel dynamical low-rank methods for solving large-scale matrix differential equations, motivated by algorithms from randomized numerical linear algebra. In terms of performance (ratio accuracy/cost), our methods can overperform existing dynamical low-rank techniques. Several applications to stiff differential equations demonstrate the robustness, accuracy and low variance of the new methods, despite their inherent randomness. Allowing augmentation of the range and corange, the new methods have a good potential for preserving critical physical quantities such as the energy, mass and momentum. Numerical experiments on the Vlasov-Poisson equation are particularly encouraging.

The new methods comprise two essential steps: a range estimation step followed by a post-processing step. The range estimation is achieved through a novel dynamical rangefinder method. Subsequently, we propose two methods for post-processing, leading to two time-stepping methods: dynamical randomized singular value decomposition (DRSVD) and dynamical generalized Nyström (DGN). The new methods naturally extend to the rank-adaptive framework by estimating the error via Gaussian sampling.