Grain boundary energy models and boundary splitting
IF 5.6
2区 材料科学
Q2 MATERIALS SCIENCE, MULTIDISCIPLINARY
引用次数: 0
Abstract
Models of grain boundary energy are essential for predicting the behavior of polycrystalline materials. Typical models represent the minimum boundary energy as a function of macroscopic boundary parameters. An energy model may allow for boundary dissociation, i.e., for a further reduction of the overall energy by splitting a boundary into two boundaries parallel to the original one. Such splitting is prevented by constraining the energy model with inequalities opposite to the boundary wetting condition. The inequalities are applicable only to triplets of boundaries that match the assumed geometric configuration. Relationships connecting the parameters of such boundaries are derived, implications of the inequalities that prevent boundary splitting are considered, and an example energy model is shown to allow boundary decomposition. Knowing whether a given energy model permits boundary dissociation and which boundaries can be affected is important for evaluating its performance in polycrystal simulations.
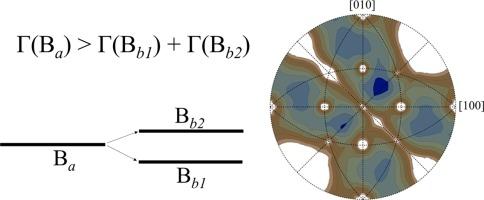
晶界能模型与晶界分裂
晶界能模型对于预测多晶材料的行为是必不可少的。典型的模型将最小边界能量表示为宏观边界参数的函数。能量模型可以允许边界解离,即通过将边界分裂成与原始边界平行的两个边界来进一步降低总能量。通过用与边界润湿条件相反的不等式约束能量模型来防止这种分裂。这些不等式只适用于与假定的几何构型相匹配的边界三元组。推导了连接这些边界参数的关系,考虑了防止边界分裂的不等式的含义,并展示了一个允许边界分解的示例能量模型。了解一个给定的能量模型是否允许边界解离以及哪些边界会受到影响,对于评估其在多晶模拟中的性能是非常重要的。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Scripta Materialia
工程技术-材料科学:综合
CiteScore
11.40
自引率
5.00%
发文量
581
审稿时长
34 days
期刊介绍:
Scripta Materialia is a LETTERS journal of Acta Materialia, providing a forum for the rapid publication of short communications on the relationship between the structure and the properties of inorganic materials. The emphasis is on originality rather than incremental research. Short reports on the development of materials with novel or substantially improved properties are also welcomed. Emphasis is on either the functional or mechanical behavior of metals, ceramics and semiconductors at all length scales.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


