Two Dimensional Non-Local Couple Stress Micropolar Thermoelasticity in Orthotropic Medium with Void using Eigen Value Approach

IF 0.9 4区工程技术 Q4 MECHANICS

Mechanics of Solids Pub Date : 2025-08-26 DOI:10.1134/S0025654425601284

Meenu Rani, Ravinder Kumar Sahrawat, Sonam Rani, Krishan Kumar

引用次数: 0

Abstract

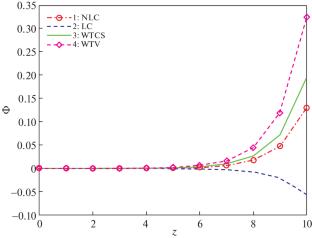
In this paper, we deal with boundary value problem in two-dimensional medium based on non-local couple stress orthotropic micropolar thermoelastic solid with voids. A traction-free insulated and isothermal boundary of a non-local thermoelastic solid are considered. The governing equations for two-dimensional problem of the medium are obtained as a vector matrix differential equation which are then solved by using eigenvalue approach. The effect of non-local, couple stress and void parameter on the displacements and temperature are computed numerically and presented graphically. Particular cases are also established and compared with the known results.

Abstract Image

查看原文本刊更多论文

基于本征值法的正交各向异性孔隙介质二维非局部耦合应力微极热弹性

本文研究了基于非局域耦合应力正交各向异性微极多孔热弹性固体的二维介质边值问题。研究了非局部热弹性固体的无牵引力绝热边界和等温边界。将介质二维问题的控制方程转化为向量矩阵微分方程，然后用特征值法求解。对非局部、耦合应力和空洞参数对位移和温度的影响进行了数值计算和图解。还建立了具体的实例，并与已知的结果进行了比较。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Mechanics of Solids 医学-力学

CiteScore

1.20

自引率

42.90%

发文量

112

审稿时长

6-12 weeks

期刊介绍： Mechanics of Solids publishes articles in the general areas of dynamics of particles and rigid bodies and the mechanics of deformable solids. The journal has a goal of being a comprehensive record of up-to-the-minute research results. The journal coverage is vibration of discrete and continuous systems; stability and optimization of mechanical systems; automatic control theory; dynamics of multiple body systems; elasticity, viscoelasticity and plasticity; mechanics of composite materials; theory of structures and structural stability; wave propagation and impact of solids; fracture mechanics; micromechanics of solids; mechanics of granular and geological materials; structure-fluid interaction; mechanical behavior of materials; gyroscopes and navigation systems; and nanomechanics. Most of the articles in the journal are theoretical and analytical. They present a blend of basic mechanics theory with analysis of contemporary technological problems.