Spontaneous modulational instability of elliptic periodic waves: The soliton condensate model
IF 2.9
3区 数学
Q1 MATHEMATICS, APPLIED
引用次数: 0
Abstract
We use the spectral theory of soliton gas for the one-dimensional focusing nonlinear Schrödinger equation (fNLSE) to describe the statistically stationary and spatially homogeneous integrable turbulence emerging at large times from the evolution of the spontaneous (noise-induced) modulational instability of the elliptic “dn” fNLSE solutions. We show that a special, critically dense, soliton gas, namely the genus one bound-state soliton condensate, represents an accurate model of the asymptotic state of the “elliptic” integrable turbulence. This is done by first analytically evaluating the relevant spectral density of states which is then used for implementing the soliton condensate numerically via a random -soliton ensemble with large. A comparison of the statistical parameters, such as the Fourier spectrum, the probability density function of the wave intensity, and the autocorrelation function of the intensity, of the soliton condensate with the results of direct numerical fNLSE simulations with initial data augmented by a small statistically uniform random perturbation (a noise) shows a remarkable agreement. Additionally, we analytically compute the kurtosis of the elliptic integrable turbulence, which enables one to estimate the deviation from Gaussianity. The analytical predictions of the kurtosis values, including the frequency of its temporal oscillations at the intermediate stage of the modulational instability development, are also shown to be in excellent agreement with numerical simulations for the entire range of the elliptic parameter of the initial potential.
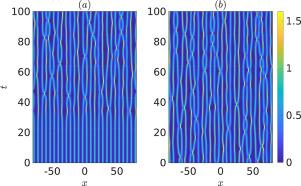
椭圆周期波的自发调制不稳定性:孤子凝聚模型
本文利用一维聚焦非线性Schrödinger方程(fNLSE)的孤子气体谱理论,描述了椭圆型“dn”fNLSE解的自发(噪声诱导)调制不稳定性演化过程中出现的大时间统计平稳和空间齐次可积湍流。我们证明了一种特殊的、临界密度的孤子气体,即一束缚态孤子凝聚体,代表了“椭圆”可积湍流渐近状态的精确模型。这是通过首先分析评估相关状态的谱密度来完成的,然后通过N大的随机N孤子系综在数值上实现孤子凝聚。孤子凝聚的统计参数,如傅里叶谱、波强度的概率密度函数和强度的自相关函数,与直接数值fNLSE模拟结果的比较表明,在没有初始数据的情况下,增加了一个小的统计均匀随机扰动(噪声),结果非常一致。此外,我们解析地计算了椭圆型可积湍流的峰度,使人们能够估计偏离高斯性。分析预测的峰度值,包括调制不稳定发展中间阶段的时间振荡频率,也显示与初始dn势的椭圆参数m的整个范围内的数值模拟非常吻合。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Physica D: Nonlinear Phenomena
物理-物理:数学物理
CiteScore
7.30
自引率
7.50%
发文量
213
审稿时长
65 days
期刊介绍:
Physica D (Nonlinear Phenomena) publishes research and review articles reporting on experimental and theoretical works, techniques and ideas that advance the understanding of nonlinear phenomena. Topics encompass wave motion in physical, chemical and biological systems; physical or biological phenomena governed by nonlinear field equations, including hydrodynamics and turbulence; pattern formation and cooperative phenomena; instability, bifurcations, chaos, and space-time disorder; integrable/Hamiltonian systems; asymptotic analysis and, more generally, mathematical methods for nonlinear systems.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


