Analysis of persistent and antipersistent time series with the Visibility Graph method

Abstract

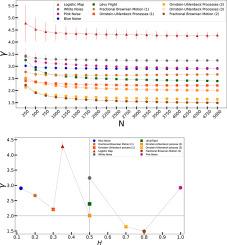
In this work, we investigate a range of time series, including Gaussian noises (white, pink, and blue), stochastic processes (Ornstein–Uhlenbeck, fractional Brownian motion, and Lévy flights), and chaotic systems (the logistic map), using the Visibility Graph (VG) method. We focus on the minimum number of data to use VG and on two key descriptors: the degree distribution $P\left(k\right)$, which often follows a power-law $P\left(k\right)\sim k^{-\gamma }$, and the Hurst exponent $H$, which identifies persistent and antipersistent time series. While the VG method has attracted growing attention in recent years, its ability to consistently characterize time series from diverse dynamical systems remains unclear. Our analysis shows that the reliable application of the VG method requires a minimum of 1000 data points. Furthermore, we find that for time series with a Hurst exponent $H\le 0.5$, the corresponding critical exponent satisfies $\gamma \ge 2$. These results clarify the sensitivity of the VG method and provide practical guidelines for its application in the analysis of stochastic and chaotic time series.