Corrections on radial edge errors of charge and current density deposition for two-dimension radial-axial particle-in-cell simulations

Abstract

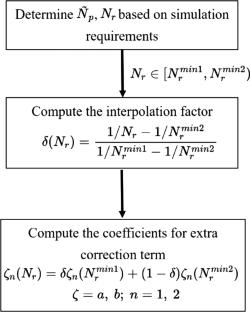
Particle-in-cell method takes an important place in plasma research and is widely used in the exploration of physical processes in various plasma devices. In the PIC method, the accuracy of the numerical results significantly depends on the density calculation of the charged particles. Density deposition algorithms for the PIC method in cylindrical coordinate system intrinsically tend to have relatively large errors at the bigger radial edge and axis. A new density deposition correction method is proposed in this paper, which performs a volume correction by calculating the area ratio of cylindrical cells, along with an additional correction factor to further improve the accuracy of density calculation. It is found that this correction factor is a function of the number of particles per cell and the number of radial cells. A set of simulation cases are carried out to provide a table of fitting function coefficients, such that the density calculation errors can be minimized. The determination of coefficients depends on the chosen simulation parameters of the number of particles and radial cells. This new method is compared to the classic Verboncoeur’s correction, and it is shown that the accuracy can be improved by several orders of magnitude.