Quantum neural network-assisted topology optimization: Concept and implementation with parameterized quantum circuits

Abstract

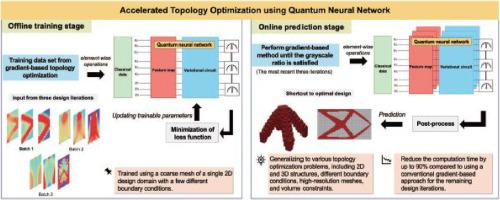
This study proposes a quantum machine learning-assisted approach to accelerating density-based topology optimization using quantum neural network (QNN), a class of trainable models based on parameterized quantum circuits (PQCs). The proposed framework extracts key features from classical data, starting by encoding the corresponding finite element analysis results, i.e., strain energy, sensitivity, and design variables from early design iterations obtained using the standard optimizer. Then, the PQCs are fine-tuned using minimization of the binary cross-entropy loss function, enabling the model to learn the mapping between input features and optimal design. Specifically, the framework consists of two main stages. First, an offline training stage where the QNN is calibrated using precomputed iterative results from a relatively coarse mesh obtained through the standard optimizer, establishing pattern recognition between input features and the final design variables. The second is an online stage where the trained QNN model is integrated with the standard optimizer to accelerate the final design. Numerical results show that QNN requires only a small number of qubits, and once trained on coarse meshes with several different boundary conditions, can effectively integrate with standard optimizers to predict target designs across various configurations, including different resolutions, volume constraints, and loading conditions. Furthermore, the proposed QNN-assisted framework significantly reduces computational time compared to standard iterative approaches, laying the groundwork for solving large-scale problems with near-term quantum computers.