Latent space modeling of parametric and time-dependent PDEs using neural ODEs
IF 7.3
1区 工程技术
Q1 ENGINEERING, MULTIDISCIPLINARY
Computer Methods in Applied Mechanics and Engineering
Pub Date : 2025-09-23
DOI:10.1016/j.cma.2025.118394
引用次数: 0
Abstract
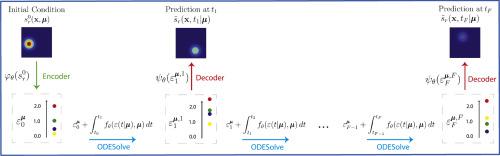
Partial Differential Equations (PDEs) are central to science and engineering. Since solving them is computationally expensive, a lot of effort has been put into approximating their solution operator via both traditional and recently increasingly Deep Learning (DL) techniques. In this paper, we propose an autoregressive and data-driven method using the analogy with classical numerical solvers for time-dependent, parametric and (typically) nonlinear PDEs. We present how Dimensionality Reduction (DR) can be coupled with Neural Ordinary Differential Equations (NODEs) in order to learn the solution operator of arbitrary PDEs accounting both for (continuous) time and parameter dependency. The idea of our work is that it is possible to map the high-fidelity (i.e., high-dimensional) PDE solution space into a reduced (low-dimensional) space, which subsequently exhibits dynamics governed by a (latent) Ordinary Differential Equation (ODE). Solving this (easier) ODE in the reduced space allows avoiding solving the PDE in the high-dimensional solution space, thus decreasing the computational burden for repeated calculations for e.g., uncertainty quantification or design optimization purposes. The main outcome of this work is the importance of exploiting DR as opposed to the recent trend of building large and complex architectures: we show that by leveraging DR we can deliver not only more accurate predictions, but also a considerably lighter and faster DL model compared to existing methodologies.
基于神经ode的参数化和时变偏微分方程的潜在空间建模
偏微分方程(PDEs)是科学和工程的核心。由于求解这些问题的计算成本很高,因此通过传统的和最近越来越多的深度学习(DL)技术,人们已经投入了大量的精力来近似它们的解算子。在本文中,我们提出了一种自回归和数据驱动的方法,利用与经典数值解的类比来求解时变、参数和(典型的)非线性偏微分方程。我们提出了如何将降维(DR)与神经常微分方程(节点)相结合,以学习任意偏微分方程的解算子,同时考虑(连续)时间和参数依赖性。我们工作的想法是,有可能将高保真度(即高维)PDE解空间映射到降维(低维)空间,该空间随后表现出由(潜在)常微分方程(ODE)控制的动态。在简化空间中求解这个(更容易的)ODE可以避免在高维解空间中求解PDE,从而减少重复计算的计算负担,例如,不确定性量化或设计优化目的。这项工作的主要成果是利用DR的重要性,而不是最近构建大型复杂架构的趋势:我们表明,通过利用DR,我们不仅可以提供更准确的预测,而且与现有方法相比,还可以提供更轻、更快的DL模型。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
12.70
自引率
15.30%
发文量
719
审稿时长
44 days
期刊介绍:
Computer Methods in Applied Mechanics and Engineering stands as a cornerstone in the realm of computational science and engineering. With a history spanning over five decades, the journal has been a key platform for disseminating papers on advanced mathematical modeling and numerical solutions. Interdisciplinary in nature, these contributions encompass mechanics, mathematics, computer science, and various scientific disciplines. The journal welcomes a broad range of computational methods addressing the simulation, analysis, and design of complex physical problems, making it a vital resource for researchers in the field.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


