Configuration-decoupled concurrent topology optimization of heterogeneous lattice structures

Abstract

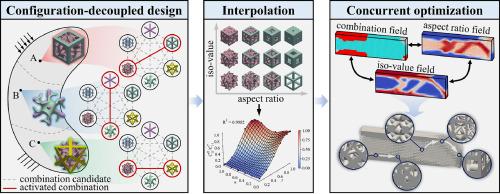
Multi-configuration lattice structures have recently been introduced into structural optimization due to their broadly tunable physical properties. Traditional methods for multi-configuration lattice optimization employ extreme strategies of complete fusion or separation, leading to a trade-off between optimality and scalability that has not been fully addressed in the existing literature. The paper suggests decomposing the lattice library into pairs of lattices, through which multi-configuration lattice optimization is decoupled into the concurrent optimization of iso-value, combination category, and ratio within combination. A novel hybrid interpolation scheme is proposed to describe the effective mechanical behavior of the configuration-decoupled lattices. In this approach, polynomial models are employed to characterize the performance of individual lattice combinations, while the Uniform Multiphase Materials Interpolation model is used to integrate the contributions of all combinations. Benchmark experiments, including full-scale simulations, are conducted to validate the effectiveness of the framework. The proposed method enables rapid convergence to configuration layouts that align with the principal stress orientations. Compared to single- and dual-configuration designs, it achieves compliance reductions of 61.0 % and 26.2 %, respectively, approaching the performance of density-based topology optimization. Extended numerical experiments reveal the joint influence of resolution and configuration count on the overall performance. This method achieves a better trade-off between optimality and extensibility, enabling more flexible utilization of large lattice databases in practical engineering fields.